Trong một cuộc thi pha chế, hai đội chơi A, B được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Đội...
Đọc tiếp
Trong một cuộc thi pha chế, hai đội chơi A, B được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Đội A pha chế được a lít nước cam và b lít nước táo và dành được điểm thưởng cao nhất. Hiệu số a-b là
A. - 6
B. 1
C. 3
D. - 1
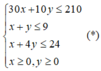
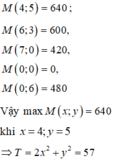
Gọi x,y lần lựợt là số lít nước cam và nước táo cần pha chế.
Số điểm thưởng nhận được là F = 60x + 80y.
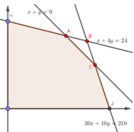
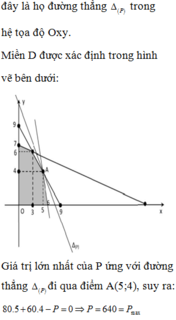
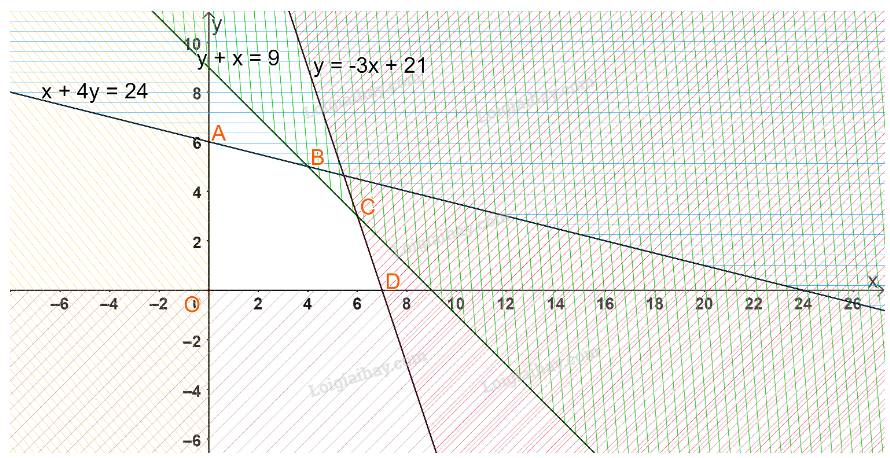
Ta có hệ BPT 30 x + 10 y ≤ 210 x + y ≤ 9 x + 4 y ≤ 24 x ≥ 0 ; y ≥ 0 . Miền nghiệm của hệ như hình vẽ.
Giá trị lớn nhất của F đạt được tại điểm (4;5). Vậy đội A đã pha chế 4 lít nước cam và 5 lít nước táo.
Đáp án D.