Cho tam giác vuông cân ABC tại A có AB= a. Tính A B → + A C →
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

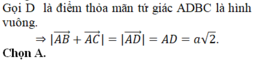

Sửa đề: cắt AB tại D.
a) Sửa đề: ΔACD=ΔECD
Xét ΔACD vuông tại A và ΔECD vuông tại E có
CD chung
\(\widehat{ACD}=\widehat{ECD}\)(CD là tia phân giác của \(\widehat{ACE}\))
Do đó: ΔACD=ΔECD(Cạnh huyền-góc nhọn)
b) Ta có: ΔACD=ΔECD(cmt)
nên DA=DE(Hai cạnh tương ứng)
Xét ΔDAE có DA=DE(cmt)
nên ΔDAE cân tại D(Định nghĩa tam giác cân)

Bn xem lại câu d nhé
`a)`
Có `Delta ABC` cân tại `A`
`=>hat(B)=hat(C)=(180^0-hat(BAC))/2`
hay `hat(B)=hat(C)=(180^0-50^0)/2`
`=>hat(B)=hat(C)=130^0/2=65^0`
`b)`
Có `H` là tđ `BC(GT)=>BH=HC`
Xét `Delta ABH` và `Delta ACH` có :
`{:(AB=AC(GT)),(AH-chung),(BH=CH(cmt)):}}`
`=>Delta ABH=Delta ACH(c.c.c)(đpcm)`
`c)`
Có `AB=AC=>A in` trung trực của `BC`(1)
`BH=CH=>H in` trung trực của `BC`(2)
Từ (1) và (2)`=>AH` là trung trực của `BC`
`=>AH⊥BC(đpcm)`


a: BC=căn 6^2+8^2=10cm
b: Xét ΔABD vuông tại A và ΔMBD vuông tại M có
BD chung
góc ABD=góc MBD
=>ΔBAD=ΔBMD
c: Xét ΔBME vuông tại M và ΔBAC vuông tại A có
BM=BA
góc MBE chung
=>ΔBME=ΔBAC
=>BE=BC
=>ΔBEC cân tại B

Bài 1
a. (Tự vẽ hình)
Áp dụng định lí Py-ta-go, ta có:
BC2= AB2 + AC2
<=> BC2= 62 + 82
<=> BC2= 100
=> BC = 10 (cm)
Bài 1
b. Áp dụng định lí Py-ta-go, ta có:
AC2 = AH2 + HC2
<=> 82 = 4,82 + HC2
<=> 64 = 23,04 + HC2
=> HC2 = 64 - 23,04
=> HC2 = 40,96
=> HC = 6,4 (cm)
=> HB = BC - HC = 10 - 6,4 = 3,6 (cm)

a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
b) Ta có: ΔABD=ΔEBD(cmt)
nên DA=DE(hai cạnh tương ứng)
Xét ΔDAE có DA=DE(cmt)
nên ΔDAE cân tại D(Định nghĩa tam giác cân)
c) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=8^2+6^2=100\)
hay BC=10(cm)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+BC+AC=8+6+10=24\left(cm\right)\)