Cho hình chóp tứ giác đều S.ABCD. Gọi M, N lần lượt là trung điểm của SA và SC.
a) Chứng minh AC ⊥ SD
b) Chứng minh MN ⊥ (SBD)
c) Cho AB = SA = a. Tính coossin của góc giữa (SBC) và (ABCD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)

a.
Do M là trung điểm SC, N là trung điểm SA \(\Rightarrow MN\) là đường trung bình tam giác SAC
\(\Rightarrow MN||AC\)
Mà \(AC\in\left(ABCD\right)\Rightarrow MN||\left(ABCD\right)\)
Gọi O là giao điểm AC và BD \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(S=\left(SAC\right)\cap\left(SBD\right)\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b.
Trong mp (ABCD), kéo dài AB và CD cắt nhau tại E
Trong mp (SCD), nối EM cắt SD tại F
\(\Rightarrow F=SD\cap\left(MAB\right)\)

Chọn B
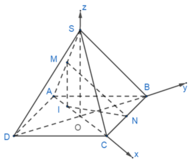
Gọi I là hình chiếu của M lên (ABCD), suy ra I là trung điểm của AO.
Khi đó
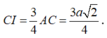
Xét tam giác CNI có
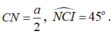
Áp dụng định lý cosin ta có:
![]()

Xét tam giác MIN vuông tại I nên
![]()
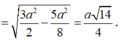
Mà MI//SO
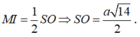
Chọn hệ trục tọa độ như hình vẽ. Ta có:
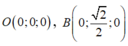
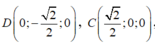
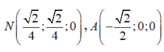
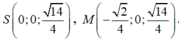
Khi đó
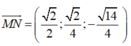
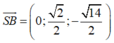
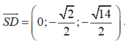
Vectơ pháp tuyến mặt phẳng (SBD)
![]()
Suy ra
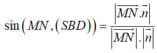
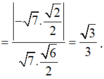

a: Xét ΔSAD có
M,N lần lượt là trung điểm của SA,SD
=>MN là đường trung bình của ΔSAD
=>MN//AD
Ta có: MN//AD
AD\(\subset\)(ABCD)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
b: Xét ΔDSB có
O,N lần lượt là trung điểm của DB,DS
=>ON là đường trung bình của ΔDSB
=>ON//SB và \(ON=\dfrac{SB}{2}\)
Ta có: ON//SB
ON\(\subset\)(OMN)
SB không thuộc mp(OMN)
Do đó: SB//(OMN)
c: Xét ΔASC có
O,M lần lượt là trung điểm của AC,AS
=>OM là đường trung bình của ΔASC
=>OM//SC
Ta có: OM//SC
OM\(\subset\)(OMN)
SC không nằm trong mp(OMN)
Do đó: SC//(OMN)
Ta có: SB//(OMN)
SC//(OMN)
SB,SC cùng thuộc mp(SBC)
Do đó: (SBC)//(OMN)
a) (AC ⊥ SH & AC ⊥ BD ⇒ AC ⊥ (SBD) ⇒ AC ⊥ SD.
b) (MN//AC & AC ⊥ (SBD) ⇒ MN ⊥ (SBD).
c) + Xác định góc α giữa (SBC) và (ABCD)
Gọi I là trung điểm của BC, ta có:
(BC ⊥ IH & BC ⊥ SH ⇒ BC ⊥ (SIH)
⇒ BC ⊥ SI.
⇒ [((SBC),(ABCD)) ] = ∠(SIH) = α.
+ Tính α:
Trong tam giác SIH, ta có: cosα = IH/IS = √3/3 ⇒ α = arccos√3/3.