Biết dãy số u n thỏa mãn u n - 1 < 1 3 với mọi n. Chứng minh rằng: l i m u n = 1 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 4 2017
Vì lim = 0 nên |
| có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
Mặt khác, ta có |un -1| < = |
| với mọi n. Nếu |un -1| có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi, nghĩa là lim (un -1) = 0. Do đó lim un = 1.
BT
26 tháng 5 2017
Có \(lim\dfrac{1}{n^3}=0\) mà \(\left|u_n-1\right|< \dfrac{1}{n^3}\) nên \(lim\left|u_n-1\right|=0\).
Suy ra: \(lim\left(u_n-1\right)=0\)\(\Leftrightarrow limu_n=1\).
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 10 2019
a/ Đặt \(x^2+65=k^2\) (\(k\in N\))
\(\Rightarrow k^2-x^2=65\)
\(\Rightarrow\left(k-x\right)\left(k+x\right)=65\)
\(\Rightarrow\left\{{}\begin{matrix}k-x=5\\k+x=13\end{matrix}\right.\) \(\Rightarrow2x=8\Rightarrow x=4\)
b/ Ta có \(8\equiv1\left(mod7\right)\Rightarrow8^n\equiv1\left(mod7\right)\)
\(\Rightarrow8^n+6\equiv7\left(mod7\right)\Rightarrow\left(8^n+6\right)⋮7\)
c/ Gọi số thợ và số ngày quy định là \(x;y\)
Theo bài ra ta có hệ:
\(\left\{{}\begin{matrix}\left(x-3\right)\left(y+6\right)=xy\\\left(x+2\right)\left(y-2\right)=xy\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}6x-3y=18\\-2x+2y=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=8\\y=10\end{matrix}\right.\)
HN
6 tháng 2 2017
Đề bài không rõ ràng. n ở đây là tự nhiên, nguyên hay là chơi luôn cả R
Đặt vn = un – 1.
Lấy số dương d > 0 bé tùy ý
⇒ luôn tồn tại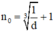
thỏa mãn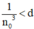 
⇒
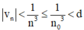với mọi n ≥ n0.
⇒ Theo định nghĩa ta có: