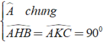Cho tam giác ABC và các đường cao BH, CK. Chứng minh Δ ABH ∼ Δ ACK.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bn tự vẽ hình nhé
a)Xét tam giác ACK và tam giác ABH:
góc K=góc H(=90độ)
AB=AC(gt)
góc A chung
vậy 2 tam giác này bằng nhau (cgv.gnk)

a) Xét \(\Delta\)ABH và \(\Delta\)ACK, có:
góc BAC chung
AB=AC(\(\Delta\)ABC cân) }=> \(\Delta\)ABH và \(\Delta\)ACK(cạnh huyền-góc nhọn)
góc K= góc H(=90 độ)
Vậy \(\Delta\)ABH và \(\Delta\)ACK
b) Vì \(\Delta\)ABH và \(\Delta\)ACK(c/m trên)
=> AK=AH(2 cạnh tg ứng)
Ta có: AB= AK+BK
AC= AH+CH
Mà AB=AC(\(\Delta\)ABC cân)
AK=AH(c/m trên)
=> BK=CK
Vậy BK=CK
c) Xét \(\Delta\)ABC, có:
BH là đường cao thứ nhất
CK là đường cao thứ hai
Mà BH cắt Ck tại I
=> I là trực tâm \(\Delta\)ABC
=> AI là đường cao \(\Delta\)ABC
=> AI vuông góc BC
Vậy AI vuông góc BC

(Tự vẽ hình)
a) Xét \(\Delta BCK\) và \(\Delta CBH\) có:
\(\widehat{BKC}=\widehat{BHC}=90^0\)
\(BC\) chung
\(\widehat{BCH}=\widehat{CBK}\) (tính chất tam giác cân)
\(\Rightarrow\Delta BCK=\Delta CBH\) (ch-gn) \(\Rightarrow BK=CH\)
b) Do \(AB=AC;BK=AH\Rightarrow AB-BK=AC-CH\Rightarrow AK=AH\)
\(\Rightarrow\dfrac{AK}{AB}=\dfrac{AH}{AC}\Rightarrow HK//BC\) (ĐL Ta - let)

xét tam giác ABC vuông tại A ( gt)
\(AB^2+AC^2=BC^2\)
=> \(BC^2=AB^2+AC^2\)
= \(21^2+28^2=1225\)
=> BC = \(\sqrt{1225}=35\left(BC>0\right)\)
VẬY BC = 35 CM

a) Xét \(\Delta ABH\)và \(\Delta ACK\)có :
\(\widehat{A}\)Chung
\(AB=AC\) ( vì tam giác ABC cân )
\(\widehat{AHB}=\widehat{AKC}=90^o\) ( GT)
Do đó tam giác ABH = tam giác ACK (cạnh huyền - góc nhọn)
b) Vì tam giác ABH = tam giác ACK ( câu a )
\(\Rightarrow CK=BH\) ( cặp cạnh tương ứng)
Xét tam giác CBK và tam giác BCH ta có :
\(BC:\)Cạnh chung
\(\widehat{BKC}=\widehat{CHB}=90^o\) (GT)
\(BC:\)Cạnh chung
Do đó tam giác CBK = tam giác BCH ( cạnh huyền - cạnh góc vuông)
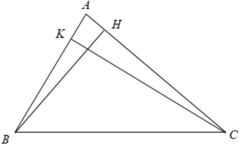
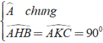
Xét Δ ABH và Δ ACK có
⇒ Δ ABH ∼ Δ ACK ( g - g )