Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Tự vẽ hình)
a) Xét \(\Delta BCK\) và \(\Delta CBH\) có:
\(\widehat{BKC}=\widehat{BHC}=90^0\)
\(BC\) chung
\(\widehat{BCH}=\widehat{CBK}\) (tính chất tam giác cân)
\(\Rightarrow\Delta BCK=\Delta CBH\) (ch-gn) \(\Rightarrow BK=CH\)
b) Do \(AB=AC;BK=AH\Rightarrow AB-BK=AC-CH\Rightarrow AK=AH\)
\(\Rightarrow\dfrac{AK}{AB}=\dfrac{AH}{AC}\Rightarrow HK//BC\) (ĐL Ta - let)

xét tam giác ABC vuông tại A ( gt)
\(AB^2+AC^2=BC^2\)
=> \(BC^2=AB^2+AC^2\)
= \(21^2+28^2=1225\)
=> BC = \(\sqrt{1225}=35\left(BC>0\right)\)
VẬY BC = 35 CM

a) Xét ΔABK vuông tại K và ΔACI vuông tại I có
\(\widehat{BAK}\) chung
Do đó: ΔABK∼ΔACI(g-g)
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AK}{AI}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AI\cdot AB=AK\cdot AC\)(đpcm)
b) Ta có: \(\dfrac{AB}{AC}=\dfrac{AK}{AI}\)(cmt)
nên \(\dfrac{AK}{AB}=\dfrac{AI}{AC}\)
Xét ΔAIK và ΔACB có
\(\dfrac{AK}{AB}=\dfrac{AI}{AC}\)(cmt)
\(\widehat{IAK}\) chung
Do đó: ΔAIK\(\sim\)ΔACB(c-g-c)

Bài làm
a) Xét tam giác ABH và tam giác ACK có:
\(\widehat{AHB}=\widehat{AKC}\left(=90^0\right)\)
\(\widehat{BAC}\) chung
=> Tam giác ABH ~ Tam giác ACK ( g - g )
b)

a: ΔEBC vuông tại E
mà EM là trung tuyến
nên EM=BC/2
ΔDBC vuông tại D
mà DM là trung tuyến
nên DM=BC/2
=>DM=EM
=>ΔMED cân tại M
b: Gọi F là trung điểm của HK
Xét hình thang BHKC có
M,F lần lượtlà trung điểm của BC,HK
nên MF là đường trung bình
=>MF//BH//CK
=>MF vuông góc HK
ΔMED cân tại M
mà MF là đường cao
nên F là trung điểm của ED
FE+EH=FH
FD+DK=FK
mà FE=FD; FH=FK
nên EH=DK
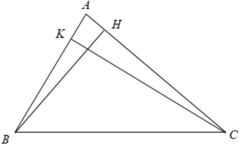
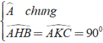
Xét Δ ABH và Δ ACK có
⇒ Δ ABH ∼ Δ ACK ( g - g )