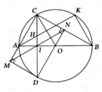
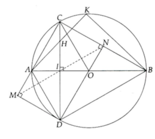
Cho đường tròn (O) đường kính AB, gọi I là trung điểm của OA, dây CD vuông góc với AB tại I. Lấy K tùy ý trên cung BC nhỏ, AK cắt CD tại H
a, Chứng minh tứ giác BIHK là tứ giác nội tiếp
b, Chứng minh AHAK có giá trị không phụ thuộc vị trí điểm K
c, Kẻ DN ^ CB, DM ^ AC. Chứng minh các đường thẳng MN, AB, CD đồng quy

a, H I B ^ = H K B ^ = 180 0
=> Tứ giác BIHK nội tiếp
b, Chứng minh được: DAHI ~ DABK (g.g)
=> AH.AK = AI.AB = R 2 (không đổi)
c, Chứng minh được MCND là hình chữ nhật từ đó => Đpcm