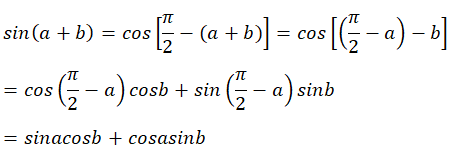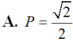Hãy chứng minh công thức sin(a + b) = sina cosb + cosa sinb.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
10 tháng 2 2019
Đúng(0)
Những câu hỏi liên quan
CM
4 tháng 3 2018
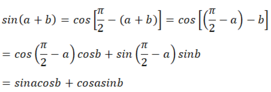
a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).
N5
1
NH
0
HP
1 tháng 7 2021
1.
\(sinA+sinB-sinC=2sin\dfrac{A+B}{2}.cos\dfrac{A-B}{2}-sin\left(A+B\right)\)
\(=2sin\dfrac{A+B}{2}.cos\dfrac{A-B}{2}-2sin\dfrac{A+B}{2}.cos\dfrac{A+B}{2}\)
\(=2sin\dfrac{A+B}{2}.\left(cos\dfrac{A-B}{2}-cos\dfrac{A+B}{2}\right)\)
\(=2sin\dfrac{A+B}{2}.2sin\dfrac{A}{2}.sin\dfrac{B}{2}\)
\(=4sin\dfrac{A}{2}.sin\dfrac{B}{2}.cos\dfrac{C}{2}\)
Sao t lại đc như này v, ai check hộ phát
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 2 2019
\(\dfrac{cosa+cos5a+cos3a}{sina+sin5a+sin3a}=\dfrac{2cos3a.cos2a+cos3a}{2sin3a.cos2a+sin3a}\)
\(=\dfrac{cos3a\left(2cos2a+1\right)}{sin3a\left(2cos2a+1\right)}=\dfrac{cos3a}{sin3a}=cot3a\)
\(\left(\dfrac{cosa}{sinb}+\dfrac{sina}{cosb}\right)\left(\dfrac{1-cos4b}{cos\left(a-b\right)}\right)=\dfrac{\left(cosa.cosb+sina.sinb\right)}{sinb.cosb}.\dfrac{2sin^22b}{cos\left(a-b\right)}\)
\(=\dfrac{cos\left(a-b\right)}{\dfrac{1}{2}sin2b}.\dfrac{2sin^22b}{cos\left(a-b\right)}=4sin2b\)
LN
0
CM
14 tháng 2 2018
Chọn C.
Theo giả thiết ta có:
P = ( sina + sinb) 2 + ( cosa + cosb) 2
= sin2a + 2.sina.sinb + sin2b + cos2a + 2cosa. cosb + cos2b
= 2 + 2( sina.sinb + cos a. cosb)
= 2 + 2.cos( a - b) ( sử dụng công thức cộng)
NT
1
17 tháng 7 2019
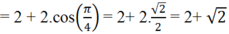
1) ta co ket qua nhu sau:
sinAcosA+cosAcosB = sinAsinB+sinAcosA
<=> cosAcosB-sinAsinB=0
<=>cos(A+B)=0
<=> -cosC=0 (vi A+B+C=180)
hay cosC=0 => C=90