Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).

ta có
sinA + sinB – sinC = 4sin (A/2) sin(B/2) cos(C/2) (2)
suy ra điều phải chứng minh.


mình làm cách này là cách khj nào mà ko cách nào khác ms làm vậy thôi, áp dụng định lí sin và cosin trong tam giác


Đặt BC = a; CA = b; AB = c.
Theo định lý hàm sin và định lý hàm cos, ta sẽ có:
\(\frac{sinB}{sinA}=\frac{b}{a};\frac{sinC}{sinA}=\frac{c}{a};\)
\(cosB=\frac{c^2+a^2-b^2}{2ca};cosC=\frac{a^2+b^2-c^2}{2ab}\).
Do đó:
\(sinA=\frac{sinB+sinC}{cosB+cosC}\)
\(\Leftrightarrow\frac{sinB}{sinA}+\frac{sinC}{sinA}=cosB+cosC\)
\(\Leftrightarrow\frac{b}{a}+\frac{c}{a}=\frac{c^2+a^2-b^2}{2ca}+\frac{a^2+b^2-c^2}{2ab}\)
\(\Leftrightarrow b+c=\frac{c^2b+a^2b-b^3+a^2c+b^2c-c^3}{2bc}\)
\(\Leftrightarrow a^2b+a^2c-b^3-c^3=b^2c+bc^2\)
\(\Leftrightarrow\left(b+c\right)\left(b^2+c^2\right)=a^2\left(b+c\right)\Leftrightarrow a^2=b^2+c^2\).
Theo định lý Pythagoras đảo, tam giác ABC vuông tại A.

1) Ta có : \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
BC \(\perp AB;BC\perp SA\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) \(\Rightarrow\Delta SBC\perp\) tại B
2) \(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) . Mà
\(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp HK\) \(\Rightarrow\Delta AHK\perp\) tại H
\(\Delta SAB\perp\) tại A ; \(AH\perp SB\) có : \(AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a^2}{\sqrt{2a^2}}=\dfrac{\sqrt{2}}{2}a\)
AC = \(\sqrt{AB^2+BC^2}=\sqrt{2a^2}=\sqrt{2}a\)
\(\Delta SAC\perp\) tại A có : \(AK\perp SC\) có :
\(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a.\sqrt{2}a}{\sqrt{a^2+2a^2}}=\dfrac{\sqrt{6}}{3}a\)
\(HK=\sqrt{AK^2-AH^2}=\sqrt{\dfrac{2}{3}a^2-\dfrac{1}{2}a^2}=\dfrac{\sqrt{6}}{6}a\)
\(S_{AHK}=\dfrac{1}{2}HA.HK=\dfrac{1}{2}\dfrac{\sqrt{2}}{2}a.\dfrac{\sqrt{6}}{6}a=\dfrac{\sqrt{3}}{12}a^2\)
3) AH \(\perp\left(SBC\right)\Rightarrow\left(AK;\left(SBC\right)\right)=\widehat{AKH}\)
\(\Delta AHK\perp\) tại H có : \(sin\widehat{AKH}=\dfrac{AH}{AK}=\dfrac{\sqrt{2}}{2}a:\dfrac{\sqrt{6}}{3}a=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{AKH}=60^o\)
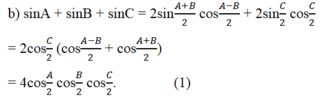
1) ta co ket qua nhu sau:
sinAcosA+cosAcosB = sinAsinB+sinAcosA
<=> cosAcosB-sinAsinB=0
<=>cos(A+B)=0
<=> -cosC=0 (vi A+B+C=180)
hay cosC=0 => C=90