Gấp hình và quan sát:
• Cắt một tam giác ABC bằng giấy với AC > AB (h.1)
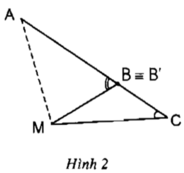
• Gấp tam giác ABC từ đỉnh A sao cho cạnh AB chồng lên cạnh AC để xác định tia phân giác AM của góc BAC, khi đó điểm B trùng với một điểm B’ trên cạnh AC (h.2).
Hãy so sánh góc AB’M và góc C.

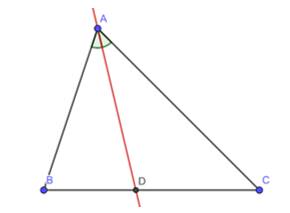
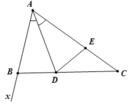
Ta có: góc AB’M là góc ngoài của tam giác MB’C
Nên ∠(BMC) + ∠C= (AB'M) ⇒ ∠(AB'M) > ∠C