Trong nửa hình cầu có OR=x(cm) ,góc (TOS) = 45 ° .Độ dài đoạn ST nhận giá trị nào trong các giá trị sau:
A.x(cm) B. 2 x(cm) C.x/ 2 cm D.2x (cm)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ tam giác vuông TOS, ta có \(ST=\dfrac{x}{\sqrt{2}}\left(cm\right)\)
Vậy ta chọn (C)

Thể tích hình nón là :
\(\dfrac{1}{3}\pi x^2.x=\dfrac{1}{3}\pi x^3\left(cm^3\right)\)
Thể tích một nửa hình cầu là :
\(\left(\dfrac{4}{3}\pi x^3\right):2=\dfrac{2}{3}\pi x^3\left(cm^3\right)\)
Vậy thể tích của hình là :
\(\dfrac{1}{3}\pi x^3+\dfrac{2}{3}\pi x^3=\pi x^3\left(cm^3\right)\)
Chọn (B)

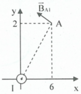
Khoảng cách từ A đến dòng điện là:
r = x 2 + y 2 = 6 2 + 2 2 = 2 10 c m
Độ lớn cảm ứng từ tại điểm A1 :
B A 1 = 2.10 − 7 . I r 1 = 2.10 − 7 . 6 2 10 .10 − 2 = 1 , 9.10 − 5 T
Chiều của vectơ cảm ứng từ B A 1 → được biểu diễn như hình vẽ.
Chọn A

Ta thấy trên nửa đường thẳng thẳng kẻ từ A và vuông góc với AB có 4 điểm theo thứ tự M, N, P, Q dao động với biên độ cực đại, nên trên AB có 9 điểm dao động với biên độ cực đai với - 4 ≤ k ≤ 4 ( d2 – d1 = kλ)
Cực đại tại M, N, P, Q ứng với k = 1; 2; 3; 4
Đặt AB = a
Tại C trên Ax là điểm dao động với biên độ cực đại:
CB – CA = kλ (*)
CB2 – CA2 = a2 → (CB + CA) (CB – CA) = a2
CB + CA = \(\dfrac{a^2}{k.\lambda}\)(**)
Từ (*) và (**) suy ra \(CA=\dfrac{a^2}{2k.\lambda}-\dfrac{k}{2}\lambda\)
Tại M: ứng với k = 1: MA = \(\dfrac{a^2}{2\lambda}\)- 0,5λ (1)
Tại N: ứng với k = 2: NA = \(\dfrac{a^2}{4\lambda}\)- λ (2)
Tại P: ứng với k = 3: PA = \(\dfrac{a^2}{6\lambda}\) - 1,5 λ (3)
Tại Q: ứng với k = 4: QA = \(\dfrac{a^2}{8\lambda}\) - 2 λ (4)
Lấy (1) – (2) : MN = MA – NA = \(\dfrac{a^2}{4\lambda}\) + 0,5λ = 22,25 cm (5)
Lấy (2) – (3) : NP = NA – PA = \(\dfrac{a^2}{12\lambda}\) + 0,5λ = 8,75 cm (6)
Lấy (5) - (6) → \(\dfrac{a^2}{\lambda}\) = 81 (cm) và λ = 4 cm .
Thế vào (4) → QA = 2,125 cm.
thầy có thể giải thích e chổ CB-CA= Klamda . Với tại s CB= K/2 lamda k thầy?

A. a + b có F = a + b
=> \(\left[ {\frac{{M.L.{T^{ - 2}}}}{{{L^2}}}} \right] = \left[ {M.{L^{ - 1}}.{T^{ - 2}}} \right]\)
B. a – b có F = a – b
=> \(\delta F = \frac{{\Delta F}}{{\overline F }} = \frac{{\Delta a + \Delta b}}{{\overline a - \overline b }} = \frac{{1 + 1}}{{51 - 49}} = 1\)
C. a x b, có F = a x b
=> \(\delta F = \delta a + \delta b = \frac{{\Delta a}}{{\overline a }} + \frac{{\Delta b}}{{\overline b }} = \frac{1}{{51}} + \frac{1}{{49}} \approx 0,04\)
D. Có F = a/b
=> \(\delta F = \delta a + \delta b = \frac{{\Delta a}}{{\overline a }} + \frac{{\Delta b}}{{\overline b }} = \frac{1}{{51}} + \frac{1}{{49}} \approx 0,04\)
Chọn B.
Ta có: OR là bán kính
Mà OR =x nên OS = x(cm)
Vậy chọn đáp án C