Hình 7.1 biểu diễn một đoạn dây dẫn AB đồng chất, tiết diện đều, hai điểm M và N chia dây dẫn AB thành ba đoạn dài bằng nhau: AM = MN = NB. Cho dòng điện cường độ I chạy qua dây dẫn này.
Hãy so sánh hiệu điện thế U A N và U M B

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì điện trở tỷ lệ với chiều dài sợi dây nên ta có:
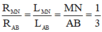
→ R A B = 3. R M N
→ U A B = I. R A B = I. R M N .3 = 3. U M N

Ta có: \(\rho_{Cu}=1,72\cdot10^{-8}\Omega.m\)
\(\rho_{Al}=2,82\cdot10^{-8}\Omega\cdot m\)
Mà hai dây dẫn cùng chiều dài, cùng tiết diện
\(\Rightarrow R_{Cu}>R_{Al}\)
\(\Rightarrow\) \(\dfrac{U_{Cu}}{I_{Cu}}>\dfrac{U_{Al}}{I_{Al}}\), hai dây cùng hiệu điện thế
\(\Rightarrow I_{Cu}< I_{Al}\)
Chọn C.

Vì Cddđ tỷ lệ thuận với tiết diện
và tỷ lên nghịch với chiều dài dây dẫn
mà cắt thành 10đoạn thì giảm 10 lần chiều dài
gập vào nhau thì tăng 10 lần tiết diện
nên cường độ dòng điện tăng giảm 10lan và vẫn giữ nguyên 2mA

\(R=\rho\dfrac{l}{S}=1,7.10^{-8}\dfrac{50}{0,34.10^{-6}}=2,5\left(\Omega\right)\)
\(I=\dfrac{U}{R}=\dfrac{220}{2,5}=88\left(A\right)\)

Điện trở của dây dẫn: \(R=\rho.\dfrac{\ell}{S}\)
Dây 1: \(R_1=\rho.\dfrac{\ell}{S_1}\)
Dây 2: \(R_2=\rho.\dfrac{\ell}{S_2}\)
Suy ra: \(\dfrac{R_1}{R_2}=\dfrac{S_2}{S_1}=3,5\)
Khi mắc dây dẫn song song vào hai điểm A, B thì hiệu điện thế hai đầu hai dây dẫn bằng nhau, suy ra:
\(U=I_1.R_1=I_2.R_2\Rightarrow \dfrac{I_2}{I_1}=\dfrac{R_1}{R_2}=3,5\)
\(\Rightarrow I_2=3,5.I_1=3,5.2=7(A)\)

Giả sử hai dòng điện I 1 và I 2 chạy ngược chiều nhau qua hai dây dẫn song song và vuông góc với mặt phẳng Hình 21.1G.
- Tại M : Vectơ cảm ứng từ B 1 — do dòng điện I 1 gây ra có gốc tại M, vuông góc với MC và có chiểu như hình vẽ. Vectơ cảm ứng từ B 2 — do dòng điện I 2 gây ra có gốc tại M, vuông góc MD và có chiều như hình vẽ.
Nhận xét thấy CMD là tam giác đều có cạnh a và góc (CMD) = 60 ° , nên góc giữa B 1 — và B 2 — tại M bằng ( B 1 — M B 2 — = 120 ° . Hơn nữa B 1 — và B 2 — lại có cùng độ lớn :
B 1 = B 2 = 2. 10 - 7 . I 1 /a = 1. 10 - 5 T
do đó vectơ cảm ứng từ tổng hợp tại M sẽ nằm trùng với đường chéo của hình bình hành và đồng thời còn là hình thoi (vì B 1 = B 2 ).
Như vậy, vectơ sẽ nằm trên đường phân giác của góc B 1 — M B 2 — hướng lên trên và có phương vuông góc với đoạn CD. Mặt khác, vì góc (BM B 1 )= (BM B 2 )= 60 ° nên tam giác tạo bởi hoặc à đều, có các cạnh bằng nhau :
B = B 1 = B 2 = 1,0. 10 - 5 T
→ U A N = I. R A N = I. R M B = U M B