Tìm số nguyên dương n thỏa mãn 1 + P 1 + 2 P 3 + 3 P 3 + . . . + n P n = P 2014 , với P n là số các hoán vị của tập hợp có n phần tử.
A. 2013
B. 2014
C. 2015
D. 2016
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{n-4}{2016}+\frac{n-3}{2015}=\frac{n-2}{2014}+\frac{n-1}{2013}\)
\(\Rightarrow\left(\frac{n-4}{2016}+1\right)+\left(\frac{n-3}{2015}+1\right)=\left(\frac{n-2}{2014}+1\right)+\left(\frac{n-1}{2013}+1\right)\)
\(\Rightarrow\frac{n-4+2016}{2016}+\frac{n-3+2015}{2015}=\frac{n-2+2014}{2014}+\frac{n-1+2013}{2013}\)
\(\Rightarrow\frac{n+2013}{2016}+\frac{n+2013}{2015}=\frac{n+2013}{2014}+\frac{n+2013}{2013}\)
\(\Rightarrow\frac{n+2013}{2016}+\frac{n+2013}{2015}-\frac{n+2013}{2014}-\frac{n+2013}{2013}=0\)
\(\Rightarrow\left(n+2013\right)\left(\frac{1}{2016}+\frac{1}{2015}+\frac{1}{2014}+\frac{1}{2013}\right)=0\)
Mà \(\frac{1}{2016}+\frac{1}{2015}+\frac{1}{2014}+\frac{1}{2013}\ne0\)
=> n + 2013 = 0 => n = -2013
Vậy n = -2013

a) Nếu n2+2014 là số chính phương với n nguyên dương thì n2 + 2014 = k2 → k2 – n2 = 2014
=> (k – n)(k + n) = 2014 (*)
Vậy (k + n) – (k – n) = 2n là số chẵn nên k và n phải cùng chẵn hoặc cùng lẻ.
Mặt khác (k – n)(k + n) = 2014 là chẵn
Nên (k – n), (k + n) đều chia hết cho 2 hay (k – n)(k + n) chia hết cho 4
Mà 2014 không chia hết cho 4
Suy ra đẳng thức (*) không thể xảy ra.
Vậy không có số nguyên dương n nào để số n2 + 2014 là số chính phương
b) Với 2 số a, b dương:
Xét: a2 + b2 – ab ≤ 1
<=> (a + b)(a2 + b2 – ab) ≤ (a + b) (vì a + b > 0)
<=> a3 + b3 ≤ a + b
<=> (a3 + b3)(a3 + b3) ≤ (a + b)(a5 + b5) (vì a3 + b3 = a5 + b5)
<=> a6 + 2a3b3 + b6 ≤ a6 + ab5 + a5b + b6
<=> 2a3b3 ≤ ab5 + a5b
<=> ab(a4 – 2a2b2 + b4) ≥ 0
<=> ab(a2 - b2) ≥ 0 đúng ∀ a, b > 0 .
Vậy: a2 + b2 ≤ 1 + ab với a, b dương và a3 + b3 = a5 + b5


n2 + n + 1 = ( m2 + m - 3 ) ( m2 - m + 5 ) = m4 + m2 + 8m - 15
\(\Rightarrow\)n2 + n - ( m4 + m2 + 8m - 16 ) = 0 ( 1 )
để phương trình ( 1 ) có nghiệm nguyên dương thì :
\(\Delta=1+4\left(m^4+m^2+8m-16\right)=4m^4+4m^2+32m-63\)phải là số chính phương
Ta có : \(\Delta=\left(2m^2+2\right)^2-4\left(m-4\right)^2-3< \left(2m^2+2\right)^2\)với m thuộc Z+
Mặt khác : \(\Delta=\left(2m^2+1\right)^2+32\left(m-2\right)\)
do đó : \(\Delta=\left(2m^2+1\right)^2+32\left(m-2\right)>\left(2m^2+1\right)^2\)với m > 2
\(\Rightarrow\left(2m^2+1\right)^2< \Delta< \left(2m^2+2\right)^2\)với m > 2
Nên ( 1 ) có nghiệm nguyên dương khi m = 1 hoặc m = 2
+) m = 1 thì \(n^2+n+16=0\) vô nghiệm
+) m = 2 thì \(n^2=n-20=0\Rightarrow\orbr{\begin{cases}n=4\left(tm\right)\\n=-5\left(loai\right)\end{cases}}\)
Thử lại m = 2 và n = 4 thỏa mãn điều kiện bài toán
Vậy m = 2 và n = 4
P/s : bài " gắt "

2) \(3^{n+2}-2^{n+2}+3^n-2^n\)
\(=2^n.3^2-2^n.2^2+3^n-2^n\)
\(=2^n.9+2^n.4+3^n-2^n\)
\(=3^n\left(9+1\right)-2^n\left(4+1\right)\)
\(=3^n.10-2^n.5\)
\(=3^n.10-2^{n-1}.10\)
\(=10.\left(3^n-2^{n-1}\right)⋮10\left(đpcm\right)\)
1) \(x+2y=3xy+3\)
\(\Rightarrow3xy+3-x-2y=0\)
\(\Rightarrow3xy-x+3-2y=0\)
\(\Rightarrow18xy-6x+18-12y=0\)
\(\Rightarrow6x\left(3y-1\right)+4-12y=-14\)
\(\Rightarrow6x\left(3y-1\right)-4\left(3y-1\right)=-14\)
\(\Rightarrow\left(6x-4\right)\left(3x-1\right)=-14\)
Bạn tự phân tích ra rồi tìm x, y nhé!
Cộng các đẳng thức ở (2) ta được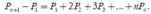
Do P 1 = 1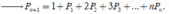
Theo đề, ta có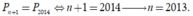
Chọn A.