Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Từ đầu bài, ta có:
M S H = 0 , 1 M T D R S H = 0 , 53 R T D
và gia tốc trọng trường trên mặt đất g=9,8m/s2
Áp dụng biểu thức tính gia tốc trọng trường ta có:
Gia tốc trọng trường trên mặt đất:
g = G M R T D 2 1
Gia tốc trọng trường trên sao Hỏa
g S H = G M S H R S H 2 2
Lấy 1 2 ta được:
g g S H = M T D R S H 2 M S H R T D 2 = M T D .0 , 53 2 R T D 2 0 , 1 M T D . R T D 2 = 2 , 809 → g S H = g 2 , 809 = 9 , 8 2 , 809 = 3 , 49 m / s 2
Đáp án: A
Chọn đáp án C
+ Gia tốc rơi tự do tại mặt dất:
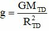
+ Gia tốc rơi tự do tại độ cao h:
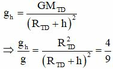
Tại mặt đất: \(g_0=G\cdot\dfrac{M}{R^2}\)
Tại độ cao h: \(g=G\cdot\dfrac{M}{\left(R+h\right)^2}\)
Xét tỉ lệ:
\(\dfrac{g_0}{g}=\dfrac{\left(R+h\right)^2}{R^2}=\dfrac{9,81}{4,9}=2\)
\(\Rightarrow\dfrac{\left(R+h\right)^2}{R^2}=2\Rightarrow h=2650,97km\)
Tại mặt đất:
\(g_0=\dfrac{GM}{R^2}\)
Tại một điểm trên bề mặt hành tinh:
\(g=\dfrac{GM'}{R'^2}=6,5\)
\(\Rightarrow\dfrac{g_0}{g}=\dfrac{M}{M'}=\dfrac{1}{6,5}=\dfrac{2}{13}\)
\(\Rightarrow M=\dfrac{2}{13}\cdot M'=\dfrac{2}{13}\cdot\dfrac{325}{10}=5kg\)
sao dap an cua de no chi ra A. 60 kg. B. 50 kg. C. 90 kg. D. 65 kg. la sao nhi
Khi vệ tinh bay quanh Trái Đất thì lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò là lực hướng tâm.
F h d = F h t ⇔ G m M r 2 = m v 2 r ⇒ v = G M r
Với: r = R + h = R + R = 2 R
Nên: v = G M 2 R
Mặt khác:
Gia tốc rơi tự do của vật ở mặt đất: g = G M R 2 ⇒ G M = g R 2
⇒ v = g R 2 2 R = g R 2 = 9 , 8.6400000 2 = 5600 m / s = 5 , 6 km / s
Đáp án: D
Chọn đáp án B
+ Thời gian rơi: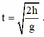
Do g chỉ còn 1/4 nên t'=2t