Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
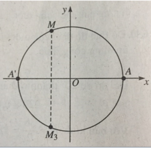
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
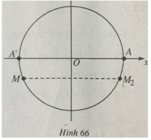
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
a, Ta đã chứng minh được: AE = b + c - a 2
=> AE = a + b + c - 2 a 2 = p – a
∆AIE có IE = EA.tan B A C ^ 2
= (p – a).tan B A C ^ 2
b, Chú ý: BI ⊥ FD và CI ⊥ E. Ta có:
B I C ^ = 180 0 - I B C ^ + I C D ^ = 180 0 - 1 2 A B C ^ + A C B ^
= 180 0 - 1 2 180 0 - B A C ^ = 90 0 + B A C ^ 2
Mà: E D F ^ = 180 0 - B I C ^ = 90 0 - α 2
c, BH,AI,CK cùng vuông góc với EF nên chúng song song => H B A ^ = I A B ^ (2 góc so le trong)
và K C A ^ = I A C ^ mà I A B ^ = I A C ^ nên H B A ^ = K C A ^
Vậy: ∆BHF:∆CKE
d, Do BH//DP//CK nên B D D C = H P P K mà DB = DF và CD = CE
=> H P P K = B F C E = B H C K => ∆BPH:∆CPK => B P H ^ = C P E ^
Lại có: B F P ^ = C E F ^ => ∆BPF:∆CEP (g.g)
mà B P D ^ = C P D ^ => PD là phân giác của B P C ^
Chọn C.
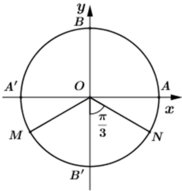
+ Cung α có mút đầu là A và mút cuối là B nên 
OMB’và ONB’ là các tam giác đều nên
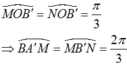
+ Cung α có mút đầu là A và mút cuối là M hoặc N nên
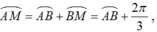
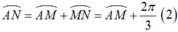
+ Chu kì của cung α là 
Từ (1), (2) ta có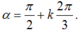 
Chọn C.
Nếu một góc lượng giác (Ou; Ov) có số đo α radian thì mọi góc lượng giác cùng tia đầu Ou, tia cuối Ov có số đo α + 2kπ, k ∈ Z, mỗi góc tương ứng với một giá trị của k.
Các cung lượng giác tương ứng trên đường tròn định hướng tâm O cũng có tính chất như vậy.