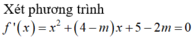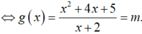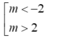Cho hàm số
f
(
x
)
=
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3
với ![]() là tham số thực. Hàm số
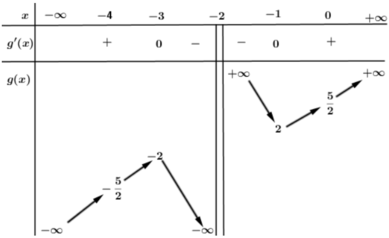
là tham số thực. Hàm số ![]() có đồ thị (C) và bảng biến thiên sau:
có đồ thị (C) và bảng biến thiên sau:
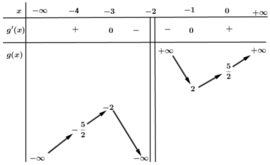
Tìm ![]() sao cho hàm số
sao cho hàm số ![]() đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn - 1
đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn - 1
A. ![]()
B. ![]()
C. ![]()
D. ![]()