Cho hàm số y = f ( x ) xác định trên D. Với x 1 , x 2 D ; x 1 > x 2 , khẳng định nào sau đây là đúng?
A. f ( x 1 ) < f ( x 2 ) thì hàm số đồng biến trên D
B. f ( x 1 ) < f ( x 2 ) thì hàm số nghịch biến trên D
C. f ( x 1 ) > f ( x 2 ) thì hàm số đồng biến trên D
D. f ( x 1 ) = f ( x 2 ) thì hàm số đồng biến trên D

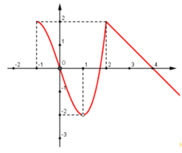

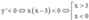
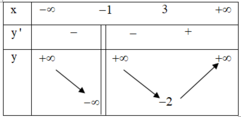


Cho hàm số y = f ( x ) xác định trên tập D. Khi đó:
- Hàm số đồng biến trên D x 1 ; x 2 D ; x 1 > x 2 f ( x 1 ) > f ( x 2 ) .
- Hàm số nghịch biến trên D x 1 ; x 2 D ; x 1 > x 2 f ( x 1 ) < f ( x 2 ) .
Đáp án cần chọn là: C