Tìm số tự nhiên a, biết rằng với mọi n ∈ N ta có an= 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: a^n=1
=>a^n=1^n
=>a=1
b: x^50=x
=>x^50-x=0
=>x(x^49-1)=0
=>x=0 hoặc x^49-1=0
=>x=0 hoặc x^49=1
=>x=0 hoặc x=1




(+) với n = 0
=> a^0 = 1 => có vô số a
(+) với n > 0
=> a^n = 1 => a = 1 ( vì 1 mũ bao nhiêu cũng bằng 1)


a, Với n = 0 => x 0 = 1 ⇒ ∀ x ∈ N
Với n ≠ 0 => x n = 1 ⇒ x = 1
b, x n = 0 => x = 0

an=1 thì có 2 trường hợp n=0 hoặc a=1
Vì với mọi n thuộc N an=1 nên a=1
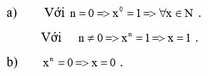
- Nếu n ≠ 0 ta có: an = a.a..a. mà an = 1 suy ra a =1
- Nếu n = 0 ta có: an = a0 = 1 đúng với mọi a ∈ N
⇒ cũng đúng với a = 1.
Vậy để an = 1 đúng với mọi n ∈ N thì a = 1