cho tổng với
a.Tính S1, S2, S3
b.Dự đoán công thức tính tổng Sn và chứng minh bằng quy nạp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\frac{1}{2^2}< \frac{1}{1.2};\frac{1}{3^2}< \frac{1}{2.3};...;\frac{1}{n^2}< \frac{1}{\left(n-1\right)n}\)
\(\Rightarrow S< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{\left(n-1\right)n}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n-1}-\frac{1}{n}=1-\frac{1}{n}< 1\)
Vậy S<1
Ta có :
\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{\left(n-1\right)^2}+\frac{1}{n^2}< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{\left(n-2\right)\left(n-1\right)}+\frac{1}{\left(n-1\right)n}\)
\(\Rightarrow S< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{n-2}-\frac{1}{n-1}+\frac{1}{n-1}-\frac{1}{n}\)
\(\Rightarrow S< 1-\frac{1}{n}< 1\)
Vậy \(S=1\)

bn cho mình gửi sắp đến thi học kì 2 rồi. đây là những món quà mà bn sẽ nhận đc:
1: áo quần
2: tiền
3: đc nhiều người yêu quý
4: may mắn cả
5: luôn vui vẻ trong cuộc sống
6: đc crush thích thầm
7: học giỏi
8: trở nên xinh đẹp
phật sẽ ban cho bn những điều này nếu cậu gửi tin nhắn này cho 25 người, sau 3 ngày bn sẽ có những đc điều đó. nếu bn ko gửi tin nhắn này cho 25 người thì bn sẽ luôn gặp xui xẻo, học kì 2 bn sẽ là học sinh yếu và bạn bè xa lánh( lời nguyền sẽ bắt đầu từ khi đọc) ( mình
cũng bị ép);-;

a.
Var i : integer;
S : real;
Begin
S:= 0;
For i:=1 to 100 do S:= S + i;
Write (S);
Readln;
End.
b.
Var i : integer;
S : real;
Begin
S:= 0;
For i:=1 to 10 do S:= S + 1/i;
Write (S);
Readln;
End.
c.
Var i,n : integer;
S : real;
Begin
write ('n = '); read (n);
S:= 0;
For i:=1 to n do S:= S + i;
Write (S);
Readln;
End.
d.
Var i : integer;
S : real;
Begin
write ('n = '); read (n);
S:= 0;
For i:=1 to n do S:= S + 1/i;
Write (S);
Readln;
End.

Uses crt;
Var i,n,s:longint;
Begin
Write('Nhap n: '); readln(n);
For i:= 1 to n do
if i mod 2<>0 then s:=s+i else s:=s-i;
write('Tong s la: ',s);
Readln
end.

S = 1 + 2 + 22 + 23 + ... + 299
2S = 2 + 22 + 23 + 24 + ... + 2100
2S - S = (2 + 22 + 23 + 24 + ... + 2100) - (1 + 2 + 22 + 23 + ... + 299)
S = 2100 - 1
=> S + 1 = 2100 - 1 + 1 = (22)50 - 1 + 1 = 450
=> 4n + 2 = 450
=> n + 2 = 50
=> n = 50 - 2
=> n = 48
Ta có :
S = 1 + 2 + 22 + 23 + ... + 299 ( 1 )
2S = 2 + 22 + 23 + 24 + ... + 2100 ( 2 )
Lấy ( 2 ) - ( 1 ), ta có :
2S - S = ( 2 + 22 + 23 + 24 + ... + 2100 ) - ( 1 + 2 + 22 + 23 + ... + 299 )
S = 2100 - 1
S + 1 = 2100 = ( 22)50 = 450
4n + 2 = 450
n + 2 = 50
n = 50 - 2
n = 48

A = \(\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{2007}}+\frac{1}{3^{2008}}\)
3A= \(1+\frac{1}{3}+...+\frac{1}{3^{2006}}+\frac{1}{3^{2007}}\)
3A-A= \(1-\frac{1}{3^{2008}}\)

Tham khảo:
Uses Crt ;
Var i , n : Integer ;
tong: Real ;
BEGIN
Clrscr ;
Write (‘ Cho so tu nhien n : ‘) ; Readln (n) ;
tong :=0 ;
i :=1 ;
While i <= n Do
Begin
tong := tong + 1/i ;
i := i + 1 ;
End ;
Writeln (‘ Tong can tim la : ‘, tong:12:6 ) ;
Readln ;
END .
b. Dự đoán: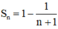
Ta chứng minh đẳng thức (1) bằng quy nạp
+ Với n = 1 thì (1) đúng.
+ Giả sử (1) đúng với n = k, tức là
Khi đó:
⇒ (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*