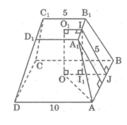
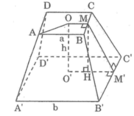
a) Tính thể tích của hình chóp đều (h.136).
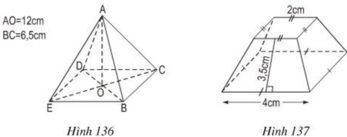
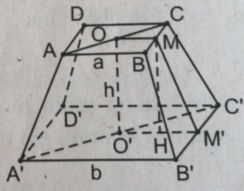
b) Tính diện tích xung quanh của hình chóp cụt đều (h.137).
(Hướng dẫn: Diện tích cần tính bằng tổng diện tích các mặt xung quanh. Các mặt xung quanh là những hình thang cân với cùng chiều cao, các cạnh đáy tương ứng bằng nhau, các cạnh bên bằng nhau).