Tìm tập xác định của các hàm số sau:
a) 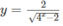
b) 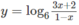
c) 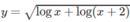
d) 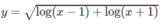
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Biểu thức \(4{x^2} - 1\) có nghĩa với mọi \(x \in \mathbb{R}\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \({x^2} + 1 \ne 0,\)tức là với mọi \(x \in \mathbb{R}\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\)
c) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(\frac{1}{x}\) có nghĩa, tức là khi \(x \ne 0,\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}{\rm{\backslash }}\{ 0\} \)

\(a,4^x-2^{x+1}\ge0\\ \Leftrightarrow2^{x+1}\le2^{2x}\\ \Leftrightarrow x+1\le2x\\ \Leftrightarrow x\ge1\)
Tập xác định của hàm số là D = \([1;+\infty)\)
\(b,\left\{{}\begin{matrix}x>0\\1-ln\left(x\right)>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>0\\ln\left(x\right)< 1\end{matrix}\right.\\ \Leftrightarrow0< x< e\)
Tập xác định của hàm số là \(\left(0;e\right)\)

a) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \( - 5x + 3 \ge 0,\)tức là khi \(x \le \frac{3}{5}.\)
Vậy tập xác định của hàm số này là \(D = ( - \infty ;\frac{3}{5}]\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(x + 3 \ne 0,\)tức là khi \(x \ne - 3\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\)

a, \(y=log\left|x+3\right|\) có nghĩa khi \(\left|x+3\right|>0\)
Mà \(\left|x+3\right|\ge0\forall x\in R\)
\(\Rightarrow\) \(\left|x+3\right|>0\) khi \(x\ne-3\)
Vậy tập xác định của hàm số là D = R \ {-3}.
b, \(y=ln\left(4-x^2\right)\) có nghĩa khi \(4-x^2>0\)
\(\Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\)
Vậy tập xác định của hàm số là D = (-2;2).

a) Tập xác đinh của hàm số \(y = \sqrt {2x - 1} + \sqrt {5 - x} \) là:
\(\left\{ {\begin{array}{*{20}{c}}{2x - 1 \ge 0}\\{5 - x \ge 0}\end{array}\,\, \Leftrightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{x \ge \frac{1}{2}}\\{x \le 5}\end{array}} \right.} \right.\,\, \Leftrightarrow \,\,\frac{1}{2} \le x \le 5\)
Vậy tập xác định của hàm số là: \(D = \left[ {\frac{1}{2};5} \right].\)
b) Tập xác định của hàm số \(y = \frac{1}{{\sqrt {x - 1} }}\) là: \(x - 1 > 0\,\, \Leftrightarrow \,\,x > 1.\)
Vậy tập xác định của hàm số là: \(D = \left( {1; + \infty } \right).\)

c: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
d: ĐKXĐ: \(x\le1\)

a) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \(2x + 7 \ge 0,\)tức là khi \(x \ge \frac{{ - 7}}{2}.\)
Vậy tập xác định của hàm số này là \(D = \left[ { - \frac{7}{2}; + \infty )} \right.\)
b) Biểu thức \(f(x)\) có nghĩa khi và chỉ khi \({x^2} - 3x + 2 \ne 0,\)tức là khi \(x \ne 2,x \ne 1.\)
Vậy tập xác định của hàm số này là \(D = \mathbb{R}\backslash \left\{ {1;2} \right\}\)

a) Biểu thức \(\frac{{1 - \cos x}}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)
b) Biểu thức \(\sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} \) có nghĩa khi \(\left\{ {\begin{array}{*{20}{c}}{\frac{{1 + \cos x}}{{2 - \cos x}} \ge 0}\\{2 - \cos x \ne 0}\end{array}} \right.\)
Vì \( - 1 \le \cos x \le 1 ,\forall x \in \mathbb{R}\)
Vậy tập xác định của hàm số là \(D = \mathbb{R}\)

a) \(y = \frac{1}{{{x^2} - x}}\) xác định \( \Leftrightarrow {x^2} - x \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne 1\end{array} \right.\)
Tập xác định \(D = \mathbb{R}\backslash \left\{ {0;1} \right\}\)
b) \(y = \sqrt {{x^2} - 4x + 3} \) xác định \( \Leftrightarrow {x^2} - 4x + 3 \ge 0 \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x \le 1\end{array} \right.\)
Tập xác định \(D = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
c) \(y = \frac{1}{{\sqrt {x - 1} }}\) xác định \( \Leftrightarrow x - 1 > 0 \Leftrightarrow x > 1\)
Tập xác định \(D = \left( {1; + \infty } \right)\)
a) Hàm số xác định khi:
4 x – 2 > 0 ⇔ 2 2 x > 2 ⇔ x > 1/2
Vậy tập xác định là D = (1/2; + ∞ )
b) D = (−2/3; 1)
c) logx + log(x + 2) ≥ 0
Vậy tập xác định là D = [−1 + 2 ; + ∞ )
d) Tương tự câu c, D = [ 2 ; + ∞ ).