Chứng tỏ rằng:
1 101 + 1 102 + 1 102 + . . . + 1 200 > 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

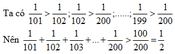


Ta có: \(\dfrac{1}{101}>\dfrac{1}{200};\dfrac{1}{102}>\dfrac{1}{200};....;\dfrac{1}{199}>\dfrac{1}{200}\)
\(\Rightarrow\dfrac{1}{101}+\dfrac{1}{102}+...+\dfrac{1}{200}>\dfrac{1}{200}+\dfrac{1}{200}+...+\dfrac{1}{200}=\dfrac{100}{200}=\dfrac{1}{2}\)
Vậy...

Ta có: 1/101 > 1/200
1/102 > 1/200
1/103 > 1/200
........
1/199 > 1/200
1/200 = 1/200
=>1/101 +1/102 +1/103 +.... +1/199 +1/200 > 1/200 + 1/200 +1/200 +..... +1/200
=>1/101 + 1/102 +1/103 +..... +1/200 > 1/200x100 = 1/2
Vậy biểu thức đã cho > 1/2

a, Đặt A = 1/101 + 1/101 + 1/103 +...+ 1/150
A là tổng 50 số giảm dần, và số nhỏ nhất là 1/150
Vậy nên A > 50 x 1/150
=> A > 1/3
b, ta có
1/101 > 1/150
1/102> 1/150
...>1/150
1/150 = 1/150
=> 1/101 + 1/102 + .... + 1/150 > 1/150 +1/150+....+1/150(50 số hạng )= 1/3
ta có
1/151 >1/200
1/152 > 1/200
..>1/200
1/200 = 1/200
=> 1/151 + 1/152+....+1/200 > 1/200+1/200+ ...+1/200( 50 số hạng) = 1/4
==> 1/101 + 1/102+....+1/200 > 1/3 +1/4
==> A > 7/12

\(S=\left(\frac{1}{101}+\frac{1}{102}+\frac{1}{103}+...+\frac{1}{150}\right)+\left(\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}\right)\)
\(S>\frac{50.1}{150}+\frac{50.1}{200}\)
\(\Rightarrow S>\frac{1}{3}+\frac{1}{4}\)
\(S>\frac{7}{12}\)
Chúc em học tốt^^
\(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{200}>\frac{7}{12}\)
\(\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{150}\right)+\left(\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}\right)\)
\(\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{150}\right)+\left(\frac{1}{151}+\frac{1}{152}+...+\frac{1}{200}\right)>\frac{50}{150}+\frac{50}{200}=\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\)

Ta có:
1/101 > 1/200
1/102 > 1/200
1/103 > 1/200
........
1/199 > 1/200
1/200 = 1/200
=>1/101 +1/102 +1/103 +.... +1/199 +1/200 > 1/200 + 1/200 +1/200 +..... +1/200
=>1/101 + 1/102 +1/103 +..... +1/200 >\(\frac{1}{200}.100\)=1/2
Vậy biểu thức đã cho > 1/2

1/Bạn thấy trong phép chia thì phép nào có số chia lớn hơn thì thương nhỏ hơn, vì vậy ps có mẫu lớn hơn thì nhỏ hơn.
2/ Ta có: Số số hạng của tổng là 200
\(\frac{1}{101}>\frac{1}{200}\)
\(\frac{1}{102}>\frac{1}{200}\)
\(...\)
\(\frac{1}{199}>\frac{1}{200}\)
\(\Rightarrow\frac{1}{101}+\frac{1}{102}+...+\frac{1}{199}>\frac{1}{200}+...+\frac{1}{200}\)
\(\Rightarrow\frac{1}{101}+\frac{1}{102}+...+\frac{1}{199}+\frac{1}{200}>\frac{1}{200}+...+\frac{1}{200}\)(mỗi bên đều 200 số hạng)
\(\Rightarrow A>\frac{1}{200}.200\)
\(\Rightarrow A>1\)

tương tự bài trước bn đưa ra
bn thử tham khảo cách lm của mik r bn tự lm nha

cái này dễ lắm chỉ là chưa để ý thôi:
a,1/101>1/102>...>1/199>1/200
=>1/101+1/102+...+1/199+1/200<100*1/101=100/101<1
các phần khác làm tương tự
đánh mỏi tay quá duyệt luôn đi