Cho tam giác ABC có AB < AC. Trên cạnh AC lấy điểm D sao cho CD = AB. Hai đường trung trực của BD và AC cắt nhau tại E. Chứng minh:
a) ∆ B E = ∆ C D E ;
b) Điểm E cách đều hai cạnh AB và AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

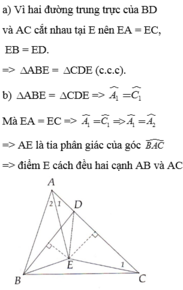

Xét hai tam giác ABE và DCE có AB=DC (giả thiết), BE=CE (vì E nằm trên trung trực BC) và EA=ED (vì E nằm trên trung trực CD). Suy ra hai tam giác bằng nhau theo trường hợp c.c.c. Từ đó suy ra góc ABE= góc DCE = góc ACE. Vậy B,C nhìn AE dưới hai góc bằng nhau, do đó ABCE nội tiếp. Suy ra E nằm trên đường tròn ngoại tiếp tam giác ABC.

a: Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>AE=DE
b: Xét ΔEAI vuông tại A và ΔEDC vuông tại D có
EA=ED
góc AEI=góc DEC
=>ΔEAI=ΔEDC
c: BI=BC
EI=EC
=>BE là trung trực của CI
=>BE vuông góc CI