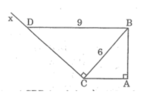
Cho tam giác ABC vuông tại A với AC = 4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Trên tia Cx lấy điểm D sao cho BD = 9cm. Chứng minh BD song song với AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
18 tháng 1 2019
Đúng(0)
Những câu hỏi liên quan
CM
5 tháng 4 2019
Xét hai tam giác vuông ABC và CDB, ta có:
∠ (BAC) = ∠ (DCB) = 90 0 (1)
Mà: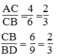
Suy ra: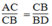 
(2)
Từ (1) và (2) suy ra: △ ABC đồng dạng △ CDB (cạnh huyền và cạnh góc vuông tỉ lệ)
Suy ra: ∠ (ACB) = ∠ (CBD)
⇒ BD//AC ( hai góc ở vị trí so le trong bằng nhau )
1 tháng 2 2018
áp dụng định lý pitago vào tam giác vuông ABC:
\(AB^2\)+\(AC^2_{ }=BC^2\)
=>\(AB^2=BC^2-AC^2\)
<=>\(AB^2=6^2-4^2=20=>AB=\sqrt[]{20}\)
ÁP dụng định lý pitago vào tam giác vuông BCD
\(BC^2+DC^2=BD^2=>DC^2=BD^2-BC^2=9^2-6^2=45=>DC=\sqrt[]{45}\)
TA CÓ
\(\dfrac{AB}{CD}=\dfrac{\sqrt[]{20}}{\sqrt[]{45}}=\dfrac{2}{3}\) (1)
\(\dfrac{DC}{BC}=\dfrac{6}{9}=\dfrac{2}{3}\) (2)
TỪ 1 và 2 => \(\Delta ABC\sim\Delta BCD\)
=>\(\widehat{DBC}=\widehat{ACB}\) mà 2 góc này ở vị trí so le trong => BD//AC
24 tháng 2 2023
a: Xét ΔBAC vuông tại A và ΔDCB vuông tại C có
BA/DC=AC/CB
=>ΔBAC đồng dạng với ΔDCB
b: ΔBAC đồng dạng với ΔDCB
=>góc ACB=góc CBD
=>AC//BD
17 tháng 12 2021
2: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
Suy ra: AD//BC