Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

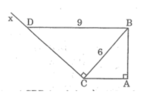
Xét hai tam giác vuông ABC và CDB, ta có:
∠ (BAC) = ∠ (DCB) = 90 0 (1)
Mà: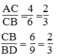
Suy ra: 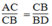 (2)
(2)
Từ (1) và (2) suy ra: △ ABC đồng dạng △ CDB (cạnh huyền và cạnh góc vuông tỉ lệ)
Suy ra: ∠ (ACB) = ∠ (CBD)
⇒ BD//AC ( hai góc ở vị trí so le trong bằng nhau )

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

Bài 1:

Áp dụng tính chất đường phân giác của tam giác ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{18}=\frac{2}{3}\)
\(\Rightarrow\frac{BD}{2}=\frac{DC}{3}=\frac{BD+DC}{2+3}=\frac{BC}{5}\Rightarrow\frac{BD}{BC}=\frac{2}{5}\)
Kẻ \(DK//BE\left(K\in AC\right)\text{ ta có:}\)
\(\frac{AE}{EK}=\frac{AI}{ID}=2;\frac{EK}{EC}=\frac{BD}{BC}=\frac{2}{5}\)
Do đó:\(\frac{AE}{EK}\cdot\frac{EK}{EC}=\frac{AE}{EC}=\frac{2}{5}.2=\frac{4}{5}\)
b)\(\text{Ta có:}\)
\(\frac{AE}{EC}=\frac{4}{5}\Rightarrow\frac{AE}{4}=\frac{EC}{5}=\frac{AE+EC}{4+5}=\frac{AC}{9}=\frac{18}{9}=2\)
\(\Rightarrow AE=8cm,EC=10cm\)
bn ơi bài 1 ý a) chỉ có thể tính tỉ lệ thôi ko tính đc ra số hẳn đâu

a: Xét ΔBAC vuông tại A và ΔDCB vuông tại C có
BA/DC=AC/CB
=>ΔBAC đồng dạng với ΔDCB
b: ΔBAC đồng dạng với ΔDCB
=>góc ACB=góc CBD
=>AC//BD

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E