Tam giác ABC có AB = AC. Trên nửa mặt phẳng bờ AB không chứa C lấy điểm M sao cho . B A M ^ = B ^ . và A M = A B . Trên nửa mặt phẳng bờ AC không chứa B lấy điểm N sao cho C A N ^ = C ^ và A N = A C . Từ A vẽ đường thẳng d ⊥ B C . Chứng tỏ rằng d là đường trung trực của đoạn thẳng MN.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác vuông ABM và tam giác vuông NCA có:
NC=AB( gt)
CA=BM ( gt)
=> Tam giác ABM = Tam giác NCA
b) Xét tam giác vuông NCA và tam giác vuông BAC có:
AC chung
NC=BA
=> Tam giác NCA =Tam giác BAC
=> ^NAC =^BCA
mà hai góc trên ở vị trí so le trong
=> NA//BC (1)
c) Xét tam giác vuông ABC và tam giác vuông BMA có:
AB chung
AC=BM
=> Tam giác vuông ABC = Tam giác vuông BMA
=> ^MAB=^ABC
mà hai góc trên ở vị trí so le trong
=> MA//CB (2)
từ (1) , (2) => N, A, M thẳng hàng
Ta lại có: NA=AM ( Tam giác ABM =tam giác NCA)
=> A là trung điểm MN

- Bạn ơi đăng câu hỏi thì đăng cho rõ ràng nhé.
- Xét tam giác AMC và tam giác NMB có:
AM=MN (gt)
Góc AMC = Góc NMB (đối đỉnh).
BM=CM (M là trung điểm BC).
=>Tam giác AMC= Tam giác NMB (c-g-c).
=>BN=AC=AE (2 cạnh tương ứng).
Góc MBN= Góc ACB (2 góc tương ứng).
Mà góc ACB+góc ABC + Góc BAC =1800 (tổng 3 góc trong tam giác ABC).
=>Góc MBN+Góc ABC+Góc BAC=1800
=>Góc ABN+ Góc BAC =1800.
- Ta có: AM=MN nên M là trung điểm AN.
- Ta có: Góc DAE + Góc DAB+ Góc BAC + Góc EAC =3600
=>Góc DAE+Góc BAC+1800=3600.
=>Góc DAE+ Góc BAC=1800
Mà góc ABN+ Góc BAC =1800 (cmt)
=>Góc DAE=Góc ABN.
- Xét tam giác DAE và tam giác ABN có:
DA=AB (gt)
Góc DAE=Góc ABN (cmt)
AE=BN (cmt)
=> Tam giác DAE=Tam giác ABN (c-g-c)
=> DE=AN (2 cạnh tương ứng) mà AM=1/2 AN (M là trung điểm AN) nên AM=1/2 DE.
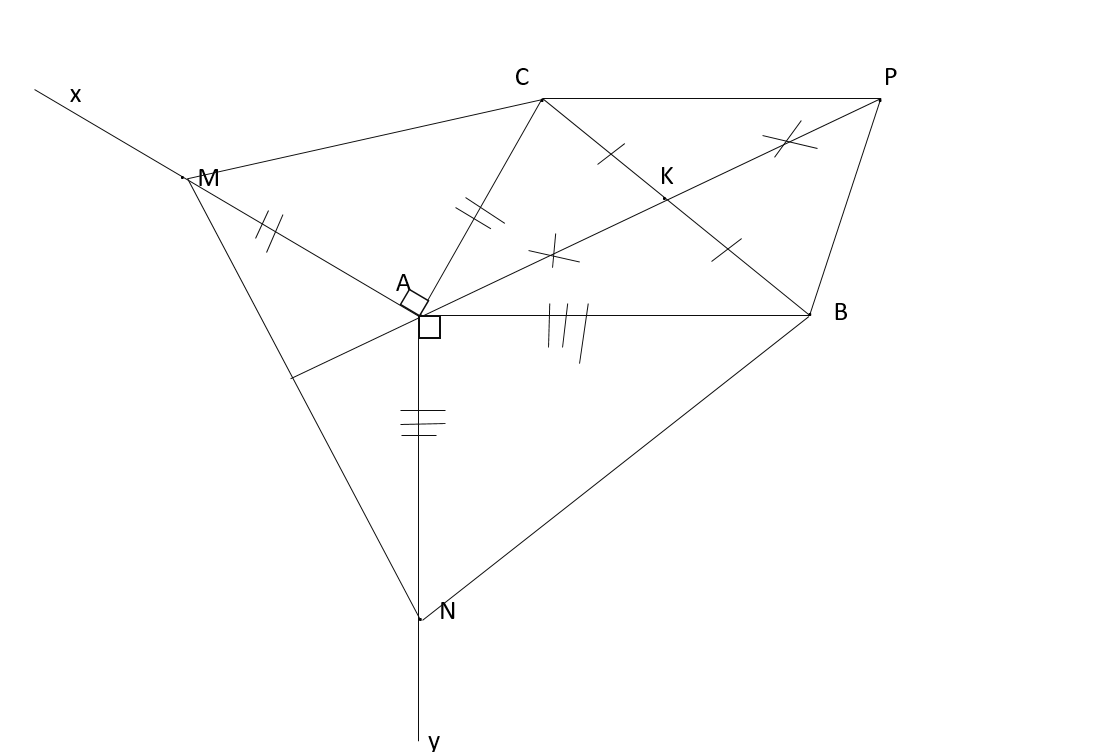
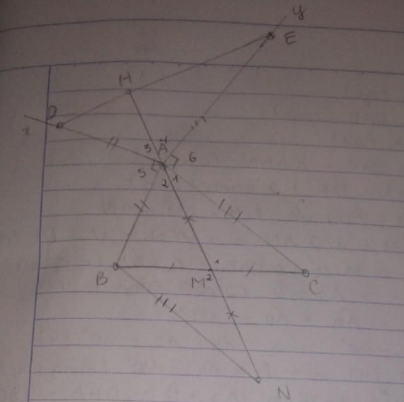
Cho tam giác ABC có A nhỏ hơn 90 độ M là trung điểm của BC trên nửa mặt phẳng có bờ AB không chứa điểm C Kẻ Ax vuông góc AB tren Ax lấy D sao cho AD =AB trên nửa mặt phẳng bờ AC không chứa điểm B Kẻ Ay vuông góc AC trên Ay lấy điểm E sao cho ae = AC Trên tia đối củaMA lấy N sao cho MN = MA Chứng minh rằng AM bằng 1/2 DE e và am bằng ô vuông góc với DE
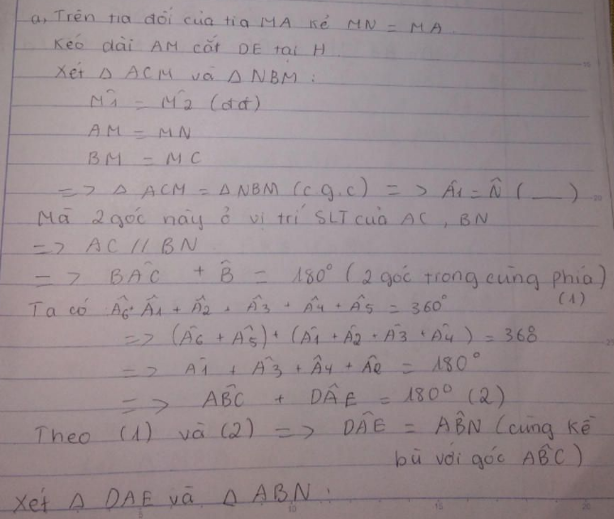
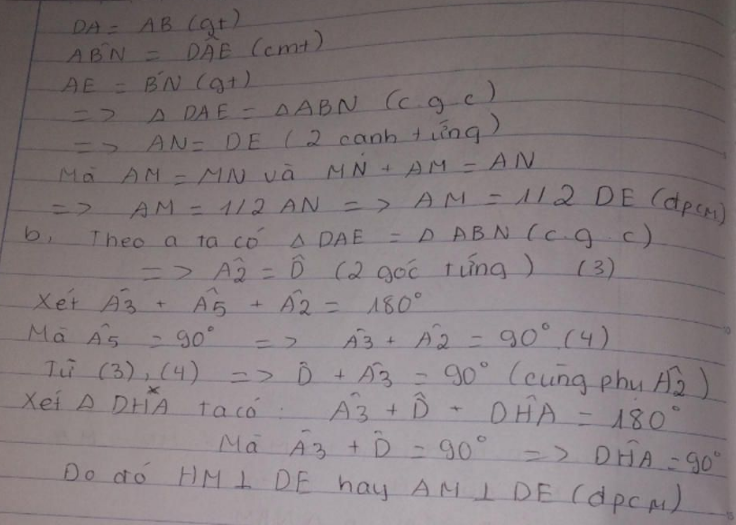
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN