Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ü Đáp án B
+ Tại t = 0, vật đi qua vị trí x=-2,5cm theo chiều dương.
→ Biễu diễn các vị trí tương ứng trên đường tròn, ta tìm được Δ t = T 6 = 1 24 s
+ Tại t = 0, vật đi qua vị trí x = -2,5 cm theo chiều dương.
→ Biễu diễn các vị trí tương ứng trên đường tròn, ta tìm được.
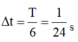
Đáp án B
Đáp án D
Bạn dùng vòng tròn để giải :
- Lúc t = 0 vật qua vị trí 1,5 cm theo chiều +, góc hợp với OX là \(\frac{\pi}{3}\)
- khi t = 0,157 s = \(\frac{\pi}{20}\) thì trên vòng tròn nó sẽ quét được góc \(\frac{\pi}{2}\) vậy góc hợp với trục ox là \(\frac{\pi}{6}\)
Vậy x = 1,5 \(\sqrt{3}\)
=> S = 1,5 + (3 - 1,5 \(\sqrt{3}\)) = 1,9
\(T=\frac{2\pi}{\omega}=\frac{157}{250}s\)
\(\Delta t=\frac{157}{1000}=\frac{T}{4}=\frac{T}{12}+\frac{T}{6}\)
Tại thời điểm t=0s vật ở vị trí \(x=\frac{A}{2}=1,5cm\) đi theo chiều âm của trục tọa độ.
Vậy quãng đường vật đi được là
\(S=\frac{A}{2}+\frac{A\sqrt{3}}{2}=\frac{3+3\sqrt{3}}{2}=4,098\approx4,1\) cm
Vậy C đúng
Chọn A
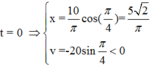
+ Thời điểm vật có vận tốc v= 20 cm/s = vmax => vật ở vị trí cân bằng x = 0.
+ Thời gian vật từ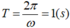 
chuyển động theo chiều âm về đến x = 0 tiếp tục chuyển động tới x = -A rồi quay về x = 0 để v = +20cm/s là 
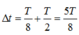mà 
=> Thời gian ngắn nhất kể từ lúc bắt đầu chuyển động đến thời điểm vật có vận tốc v = 20 cm/s là 5/8 (s).
Chọn D
+ T = 2 π w = 2 π 2 π = 1 s
+ t = 0: x = 2cosπ = -2cm => chất điểm ở vị trí biên âm.
+ x = 3 cm = A 3 2
+ Sử vòng tròn: tmin = t-A→O + tO→ A 3 /2 = T 4 + T 6 = 5 T 12 = 5 12 s.