Đo chiều dài của một cây cầu, ta được số đo a = 192,55m, với sai số tương đối không vượt quá 0,2%. Giá trị gần đúng của chiều dài cây cầu là:
A. 195m.
B. 192m.
C. 191m.
D. 193m.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Sai số tuyệt đối là: \(\Delta = \left| {e - 2,7} \right| = \;|2,718281828459 - 2,7|\; = 0,018281828459 < 0,02\)
Sai số tương đối là: \({\delta _a} = \frac{{{\Delta _a}}}{{|a|}} < \frac{{0,02}}{{2,7}} \approx 0,74\% \)
b) Quy tròn e đến hàng phần nghìn ta được: 2,718.
c)
Hàng của chữ số khác 0 đầu tiên bên trái của d = 0,00002 là hàng phần trăm nghìn.
Quy tròn e đền hàng phầm trăm nghìn ta được 2,71828

a) Xét: | π - 3,14 | = π - 3,14 < 3,1416 - 3,14 = 0,0016 < 0,002
b) |π - 3,1416 I = 3,1416 - π < 3,1416 - 3,1415 = 0,0001
Chúc bạn học tốt ~
a) Xét: | π - 3,14 |
= π - 3,14 < 3,1416 - 3,14 = 0,0016 < 0,002
b) |π - 3,1416 I = 3,1416 - π < 3,1416 - 3,1415
= 0,0001

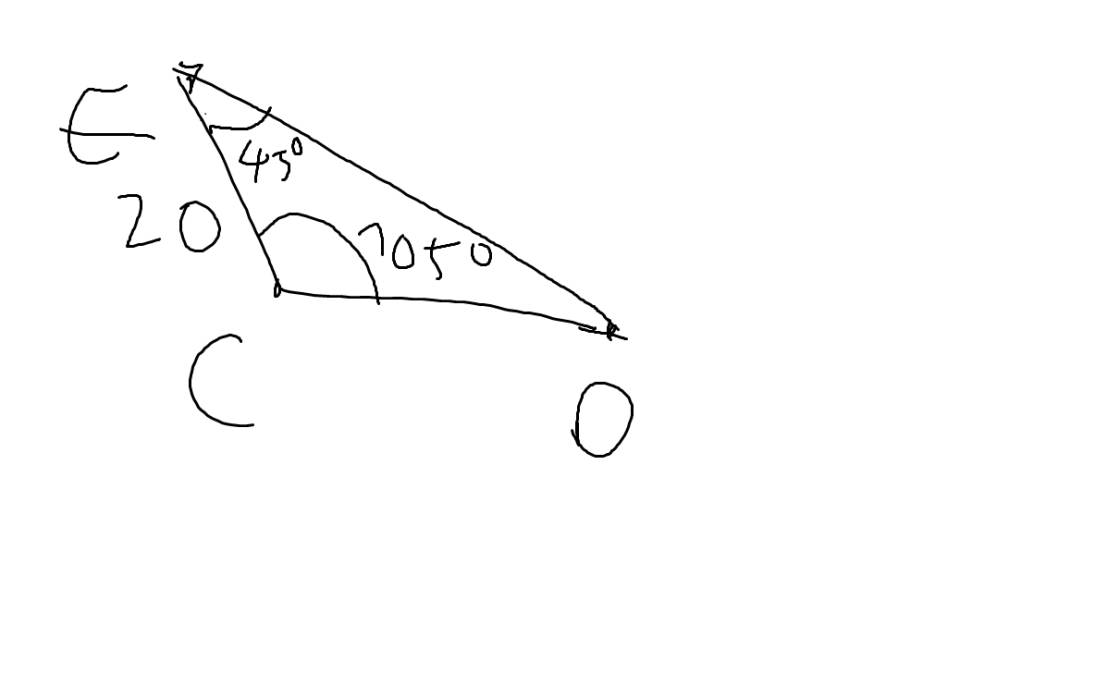
Xét ΔCED có \(\widehat{C}+\widehat{D}+\widehat{E}=180^0\)
=>\(\widehat{D}+105^0+45^0=180^0\)
=>\(\widehat{D}=30^0\)
Xét ΔCED có \(\dfrac{CE}{sinD}=\dfrac{CD}{sinE}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{sin30}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{\dfrac{1}{2}}=40\)
=>\(CD=40\cdot sin45=40\cdot\dfrac{\sqrt{2}}{2}=20\sqrt{2}\)

Ta có: l = 1745,25m ± 0,01m có độ chính xác đến hàng phần trăm (độ chính xác là 0,01) nên ta quy tròn số đến hàng phần chục.
Vậy số quy tròn của 1745,25m là 1745,3 m.

0,7 km = 700 met và 1/4 phút = 15 giây.
Ta có Vận tốc = quảng đường chia cho thời gian.
Vận tốc của tàu là = 700 chia cho 50 s = 14 m/s
Chiều dài của tàu là l = vận tốc nhân cho thời gian
l = 14 X 15 = 210 mét
Trả lời:
a) Đổi 1/4 phút =1 5 giây
0,7 km =700 m
Thời gian xe lửa đi được là:
50-15=35(giây)
Vận tốc của xe lửa là:
700:35=20(m/giây)
Chiều dài xe lửa = 15 x 20=300m
b) Đổi 10,8 km/giờ = 3m/giây
Điểm cuối xe lửa là điểm di chuyển ngược chiều để gặp nhau với xe đạp trên quãng đường 195m.
Sau 15 giây xe đạp đi được: 3 x 15 = 45 (m)
Quãng đường còn lại xe lửa đi: 195 – 45 = 150 (m)
Vận tốc xe lửa: 150 : 15 = 10 (m/giây)
Đáp số: 10 m/giây = 36km/giờ

Đáp án B
Ban đầu ta cần phải treo con lắc đơn lên giá tại nơi cần xác định gia tốc trọng trường g. Sau đó dùng thước đo 5 lần chiều dài l của dây treo từ điểm treo tới tâm vật. Tiếp theo kích thích cho vật nhỏ dao động, rồi dùng đồng hồ bấm giây để đo thời gian của một dao động toàn phần để tính được chu kỳ T, lặp lại phép đo 5 lần. Dựa vào công thức trung bình tính giá trị trung bình của chiều dài và chu kỳ sau đó thay vào công thức để tính gia tốc trọng trường trung bình tại ví trí đó.

(Các bạn tự đo chiều dài lớp học của mình rồi tính toán kết quả).
Ví dụ : Số đo lớp học sau 5 lần đo lần lượt là : 8,24m ; 8,19m ; 8,25m ; 8,3m ; 8,27m.
Vậy chiều dài lớp học gần đúng nhất là : (8,24+8,19+8,25+8,3+8,27) :5 = 8,25(m).
Đáp án: D
Ta có sai số tuyệt đối của số đo chiều dài con dốc là :
Δa = a . δ a = 182,55. 0,2% = 0.3851.
Vì 0.05 < Δa < 0,5 . Do đó chữ số chắc của d là 1, 9, 2.
Vậy cách viết chuẩn của a là 193m (quy tròn đến hàng đơn vị).