Biết đường thẳng y= (3m-1) x+ 6m+3 cắt đồ thị hàm số y= x3-3x2+ 1 tại ba điểm phân biệt sao cho một giao điểm cách đều hai giao điểm còn lại. Khi đó m thuộc khoảng nào dưới đây?
A. (1; 3/2)
B. (0;1)
C. (-1; 0)
D. (3/2; 2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Giả thiết bài toán ó điểm uốn của đồ thị hàm số y = x3 – 3x2 + 1 thuộc đường thẳng. Mặt khác ![]()
<=> ![]()
Với ![]() thử lại thấy thỏa mãn nên
thử lại thấy thỏa mãn nên ![]() là giá trị cần tìm
là giá trị cần tìm

Đáp án C.
Phương trình hoành dộ giao điểm của (C) và (d) là
3 m − 1 x + 6 m + 3 = x 3 − 3 x 2 + 1 ⇔ x 3 − 3 x 2 − 3 m − 1 x − 6 m − 2 = 0 ( * ) .
Giả sử A x 1 ; y 1 , B x 2 ; y 2 và C x 3 ; y 3 lần lượt là giao điểm của (C) và (d).
Vì B cách đều 2 điểm A, C ⇒ B là trung
điểm của AC ⇒ x 1 + x 3 = 2 x 2 .
Mà theo định lí Viet cho phương trình (*), ta được
x 1 + x 2 + x 3 = 3 → 3 x 2 = 3 ⇒ x 2 = 1.
Thay x 2 = 1 vào (*), ta có
1 3 − 3.1 2 − 3 m − 1 − 6 m − 2 = 0 ⇔ − 9 m − 3 = 0 ⇔ m = − 1 3 .
Thử lại, với m = − 1 3 ⇒ ( * ) ⇔ x 3 − 3 x 2 + 2 x = 0
⇔ x = 0 x = 1 x = 2 (TM)
Vậy m ∈ − 1 ; 0 .

Chọn B
Phương trình hoành độ giao điểm ![]()
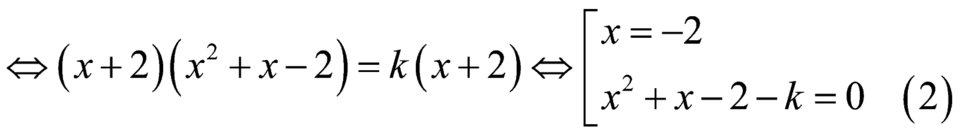 .
.
Đường thẳng![]() cắt đồ thị hàm số
cắt đồ thị hàm số ![]() tại
tại ![]() điểm phân biệt
điểm phân biệt
![]() có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác ![]()

![]()
Giả sử ![]() ,
, ![]() là hai nghiệm phân biệt của
là hai nghiệm phân biệt của ![]() , theo hệ thức Viet thì
, theo hệ thức Viet thì 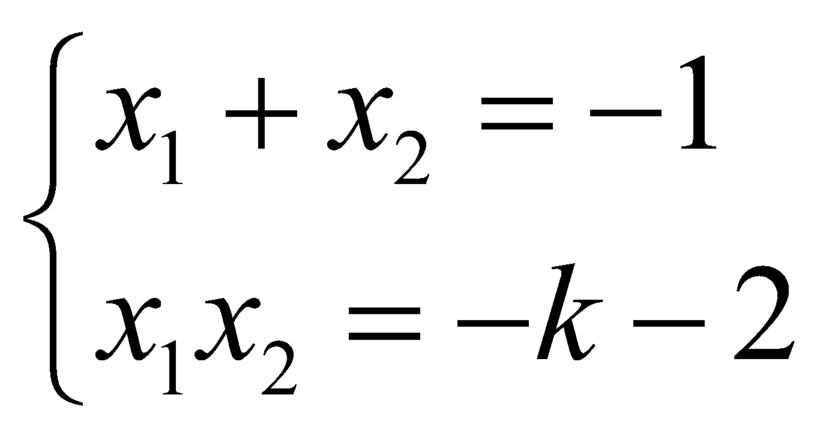 .
.
Ta có 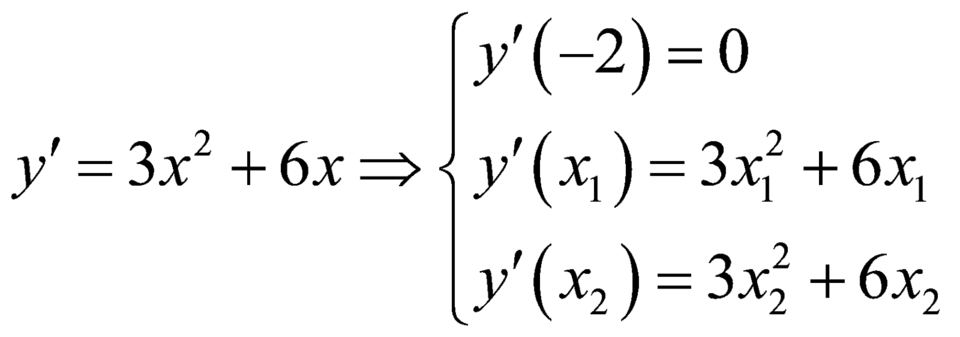 .
.
Bài ra ta có 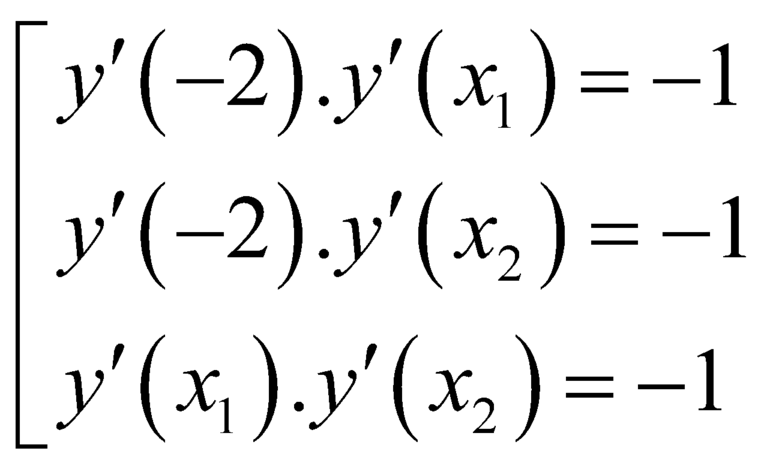
![]()
![]()
![]()
![]() .
.
Kết hợp với ![]() ta được
ta được ![]() thỏa mãn.
thỏa mãn.

Đáp án A
Hoành độ giao điểm của đt y = x - 1 và đồ thị y = x 3 - 3 x 2 + 4 = 0 là nghiệm của PT
x 3 - 3 x 2 + x + 3 = x - 1 ⇔ ( x + 1 ) ( x - 2 ) 2 = 0 ⇔ x 1 = - 1 x 2 = 2 ⇒ y 1 = - 2 y 2 = 1 ⇒ y 1 + y 2 = - 1
PT hoành độ giao điểm là
(3m-1) x+ 6m+ 3 == x3-3x2+ 1 hay x3-3x2 – (3m-1) x-6m-2=0 ( *)
Giả sử A( x1; y1) ; B( x2; y2) lần lượt là giao điểm của (C) và (d)
Vì B cách đều hai điểm A và C nên B là trung điểm của AC
Suy ra x1+ x3= 2x2
Thay x2= 1vào , ta có
Vậy -1< m< 0
Chọn C.