Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Lập phương trình hoành độ giao điểm của hai đồ thị hàm số, tìm hoành độ giao điểm hoặc áp dụng định lý Vi-et để tính giá trị biểu thức đề bài yêu cầu.
Cách giải:


Đáp án C
PT hoành độ giao điểm là
x x − 1 = x − 2 ⇔ x − 1 ≠ 0 x 2 − 3 x + 2 = x ⇔ x ≠ 1 x 2 − 4 x + 2 = 0 ⇒ x 2 − 4 x + 2 = 0
Suy ra x A + x B = 4
Gọi G là trọng tâm tam giác O A B ⇒ x G = x A + x B + x O 3 = 4 3

Đáp án A
PT hoành độ giao điểm là x + 1 = x + 3 x − 1 ⇔ x ≠ 1 x 2 − x − 4 = 0 , Δ = 17 > 0 ⇒ x A + x B = 1 y A + y B = − 4
Suy ra A x A ; x A + 1 B x B ; x B + 1 ⇒ A B = 2 x A − x B 2 = 2 x A + x B 2 − 8 x A x B = 2 1 2 − 8 − 4 = 34

Đáp án A
PT hoành độ giao điểm là x − 2 = 2 x + 1 x − 1 ⇔ x ≠ 1 x 2 − 3 x + 2 = 2 x − 1 ⇔ x ≠ 1 x 2 − 5 x + 3 = 0 ⇒ x A + x B = 5.



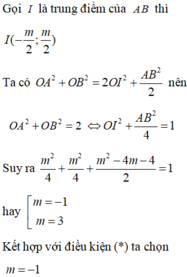




Đáp án A
Hoành độ giao điểm của đt y = x - 1 và đồ thị y = x 3 - 3 x 2 + 4 = 0 là nghiệm của PT
x 3 - 3 x 2 + x + 3 = x - 1 ⇔ ( x + 1 ) ( x - 2 ) 2 = 0 ⇔ x 1 = - 1 x 2 = 2 ⇒ y 1 = - 2 y 2 = 1 ⇒ y 1 + y 2 = - 1