Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x − 1 2 = y + 1 − 1 = z 3 và mặt phẳng ( α ) : x + 5 y + z + 4 = 0. Xác định vị trí tương đối của d và ( α )
A. d ⊥ ( α ) .
B. d ⊂ ( α ) .
C. d cắt và vuông góc với α
D. d / / ( α ) .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Gọi giao điểm của Δ và d là B nên ta có: B (3+t;3+3t;2t) ![]()
Vì đường thẳng Δ song song với mặt phẳng (α) nên:
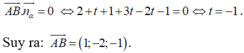
Phương trình đường thẳng Δ đi qua A và nhận 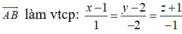

Đáp án D
Đường thẳng d 1 đi qua M 1 1 ; − 2 ; − 1 và có VTCP u 1 → = 3 ; − 1 ; 2 .
Đường thẳng d 2 đi qua M 2 12 ; 0 ; 10 và có VTCP u 2 → = − 3 ; 1 ; − 2 .
Như vậy: u 1 → = − u 2 → , M 1 ∉ d 2 . Suy ra d 1 / / d 2 .
Chú ý: Hai đường thẳng d 1 và d 2 song song nên em không thể lấy tích có hướng của hai VTCP để tìm VTPT của mặt phẳng vì tích có hướng của hai vectơ cùng phương là vectơ-không.
Gọi n → là một VTPT của mặt phẳng α thì vuông n → góc với hai vectơ không cùng phương


Chọn A

mặt khác M(1;−2;−1) thuộc d, M thuộc (α).
Vậy đường thẳng d thuộc mặt phẳng (α).

Đáp án B
Phương pháp giải:
Ứng dụng của tích có hướng để tìm vectơ pháp tuyến của mặt phẳng. Phương trình mặt phẳng đi qua M ( x 0 ; y 0 ; z 0 ) và có VTPT
![]()
![]()
Lời giải:
![]()
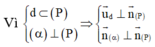
![]()
![]()
Vậy phương trình mặt phẳng (P): 2x-3y-z+7=0