Cho hình vẽ dưới đây.
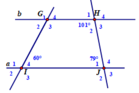 a. Chứng minh rằng a // b
a. Chứng minh rằng a // b
b. Tính số đo góc G 1 ^ , G 2 ^ , G 3 ^ , G 4 ^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tập xác định của hàm số đã cho là: \({D_f} = \mathbb{R};\;{D_g} = \mathbb{R}\)
b) Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\)
Đồ thị của hàm số \(y = f\left( x \right) = {x^2}\) đối xứng qua trục tung
c) Ta có: \(g\left( { - x} \right) = {\left( { - x} \right)^3} = - {x^3} = - g\left( x \right)\)
Đồ thị của hàm số \(y = g\left( x \right) = {x^3}\) đối xứng qua gốc tọa độ

Lời giải:
Kéo dài $BG$ cắt $AC$ tại $K$. Kẻ $KK'\perp d$
Trên $BG$ lấy trung điểm $I$. Kẻ $II'\perp d$
Vận dụng công thức đường trung bình trong hình thang ta có:
Xét hình thang $BGG'B'$ có đtb $II'$ thì:
$II'=\frac{BB'+GG'}{2}(1)$
Xét hình thang $AA'C'C$ có đường trung bình $KK'$ thì:
$KK'=\frac{AA'+CC'}{2}(2)$
Xét hình thang $II'KK'$ có đường trung bình $GG'$ thì:
$GG'=\frac{II'+KK'}{2}(3)$
Từ $(1);(2);(3)$ suy ra:
$GG'=\frac{BB'+GG'+AA'+CC'}{4}$
$\Rightarrow GG'=\frac{AA'+BB'+CC'}{3}$
Ta có đpcm.

a: Vì góc aMN=góc MNQ
nên aa'//bb'
b: góc PQN=180-100=80 độ=góc b'Qd'
góc b'Qd=d'QN=180-80=100 độ

a) ta có: đường thẳng AB,CD cắt nhau tại O
=> góc AOC = góc BOD = 60 độ ( đối đỉnh)
=> góc BOD = 60 độ
mà góc BOD + góc BOC = 180 độ ( kề bù)
thay số: 60 độ + góc BOC = 180 độ
góc BOC = 180 độ - 60 độ
góc BOC = 120 độ
mà góc BOC = góc AOD = 120 độ ( đối đỉnh)
=> góc AOD = 120 độ
b) ta có: Ot là tia phân giác của góc AOC
ma Ot là tia đối của tia Ot'
=> tt' là tia phân giác của góc AOC
mà góc AOC = góc BOD ( đối đỉnh)
=> tt' là tia phân giác của góc BOD
mà Ot nằm giữa OA;OC và Ot là tia đối của Ot', góc AOC = góc BOD đối đỉnh
=> Ot' nằm giữa OB,OD
mà Ot' thuộc tt'
=> Ot' là tia phân giác của góc BOD
C O B D A t t' 60

a, HCDB là hbh (gt)
-> CH // BD; HB // CD
Vì H là trực tâm của Δ ABC (gt)
-> CH vuông với AB ; BH vuông với AC ; AH vuông với BC
-> AB vuông BD ; AC vuông CD
-> ^ABD=90*, ^ ACD=90*
Xét tứ giác ABCD có: ^ABD + ^ ACD = 180*
-> tứ giác ABCD nội tiếp
-> A, B, C, D cùng thuộc 1 đường tròn (1)
DE // BC (gt)
->AH vuông DE ( vì AH vuông BC )
-> ^AED = 90*
Xét tứ giác ABED có ^AED=^ABD=90*
-> B và E cùng nhìn AD dưới 1 góc 90*
-> ABED nội tiếp
-> A,B,E,D cùng thuộc 1 đường tròn (2)
Từ (1) và (2) -> A,B,C,D,E cùng thuộc một đường tròn
b) ABEDC nội tiếp
-> ^BAE = ^BDE (2 góc nội tiếp cùng chắn cung BE)
Và ^DAC = ^DBC (2 góc nội tiếp cùng chắn cung CD)
Mà ^DBC = ^BDE (2 góc sole trong)
-> ^BAE = ^CAD
a. H 2 ^ + J 1 ^ = 101 ° + 79 ° mà 2 góc này ở vị trí trong cùng phía => a // b
b. a / / b ⇒ G 4 ^ = I 4 ^ (đồng vị) ⇒ G ^ 1 = G 3 ^ = 120 ° ; G ^ 4 = G ^ 2 = 60 °