Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
a) Chứng minh rằng: BM // DN.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 12 2019
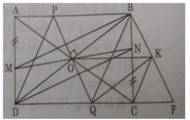
c) PQ ⊥ BD (gt). Xét các tam giác vuông POB và QOD có:
∠POB = ∠QOD∠ (đối đỉnh),
OB = OD
∠PBO = ∠QDO (so le trong).
Do đó ΔPOB = ΔQOD (g.c.g) ⇒ BP = DQ
Lại có BP // DQ nên tứ giác PBQD là hình bình hành
Mặt khác PBQD có hai đường chéo vuông góc nên là hình thoi.
CM
16 tháng 8 2019
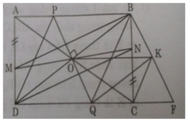
b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.
Lại có tứ giác BMDN là hình bình hành nên MN phải đi qua trung điểm O của BD.
Vậy AC, BD, MN đồng quy tại O.
CM
12 tháng 10 2019
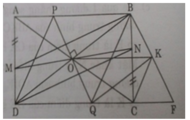
d) Gọi F là giao điểm của BK và QC. Ta có O là trung điểm của BD và OQ // BK (gt) nên Q là trung điểm của DF.
Lại có QK // BD (gt); Q là trung điểm của DF ⇒ K là trung điểm của BF.
CK là trung tuyến của tam giác vuông BCF ⇒ CK = BK = BC/2.
Ta có QK là đường trung bình của tam giác
⇒ QK = BO = BD/2; QK // BO
⇒ Tứ giác OBKQ là hình bình hành
Mặt khác ∠(OBQ) = 90o ⇒ OBKQ là hình chữ nhật
⇒ ∠(OBK) = 90o
Xét ΔOCK và ΔOBK có
CK chung
OC = OB (tính chất đường chéo hình chéo hình chữ nhật)
CK = BK (cmt)
Vậy ΔOCK = ΔOBK (c.c.c) ⇒ ∠OCK = ∠OBK = 90o hay AC ⊥ CK.
H
22 tháng 8 2023
.a.
Vì `EF` là đường trung trực MB.
=> `EM=EB`
=> `ΔEMB` cân tại E
=> \(\widehat{EMB}=\widehat{EBM}\)
Chứng minh tương tự được: \(\widehat{FMB}=\widehat{FBM}\)
Vì `AM=DN` mà AM//DN
=> Tứ giác `AMND` là hình bình hành.
b.
Từ câu (a) suy ra:
ME//BF
BE//FM
=> Hình bình hành MEBF có `EF⊥MB`
=> Tứ giác MEBF là hình thoi
10 tháng 3 2022
-OM cắt DC tại N'.
\(\dfrac{AM}{DN}=\dfrac{MB}{NC}=\dfrac{AM+MB}{DN+BC}=\dfrac{AB}{DC}\)
-Xét △ODN' có: AM//DN'.
\(\Rightarrow\dfrac{AM}{DN'}=\dfrac{OM}{MN'}\) (hệ quả định lí Ta-let) (1)
-Xét △OCN' có: BM//CN'.
\(\Rightarrow\dfrac{BM}{CN'}=\dfrac{OM}{MN'}\) (định lí Ta-let) (2)
-Từ (1) và (2) suy ra:
\(\dfrac{AM}{DN'}=\dfrac{BM}{CN'}=\dfrac{AM+BM}{CN'+DN'}=\dfrac{AB}{CD}\)
\(\Rightarrow\dfrac{AM}{CN'}=\dfrac{BM}{DN'}=\dfrac{AM}{CN}=\dfrac{BM}{DN}\)
\(\Rightarrow CN=CN';DN=DN'\)
\(\Rightarrow N\equiv N'\)
-Vậy MN đi qua điểm O.
a) Ta có AD = BC; AD // BC (gt), AM = CN (gt)
⇒ AD – AM = BC – CN
Hay DM = BN
Lại có DM // BN
Do đó MNDN là hình bình hành ⇒ BM // DN