Cho biết
cos α + sin α cos α - sin α = 5
Tính tanα
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1:
a: sin a=căn 3/2
\(cosa=\sqrt{1-sin^2a}=\sqrt{1-\dfrac{3}{4}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)
\(tana=\dfrac{\sqrt{3}}{2}:\dfrac{1}{2}=\sqrt{3}\)
cot a=1/tan a=1/căn 3
b: \(tana=2\)
=>cot a=1/tan a=1/2
\(1+tan^2a=\dfrac{1}{cos^2a}\)
=>\(\dfrac{1}{cos^2a}=5\)
=>cos^2a=1/5
=>cosa=1/căn 5
\(sina=\sqrt{1-cos^2a}=\sqrt{\dfrac{4}{5}}=\dfrac{2}{\sqrt{5}}\)
c: \(cosa=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
tan a=5/13:12/13=5/12
cot a=1:5/12=12/5

Chọn B.
Ta có: 1 + cos2α = 2cos2α và sin2α = 2sinα.cosα.
Mà tanα = 2 nên cot α = 1/2
Suy ra:
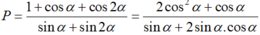
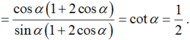

Để giải bài toán này, ta sẽ sử dụng các công thức và quy tắc trong lượng giác để tính toán.
Trước hết, ta có: sin(α+β) = sinα.cosβ + cosα.sinβ cos(α+β) = cosα.cosβ - sinα.sinβ
Đề bài cho α+β = 1313 và tanα = -2tanβ. Ta có thể suy ra các thông tin sau: tanα = -2tanβ => sinα/cosα = -2sinβ/cosβ => sinα.cosβ = -2sinβ.cosα
Bài toán yêu cầu tính A = sin(α+3π/8) . cos(α+π/8) + sin(β-5π/12) . sin(β-π/12)
Để tính A, ta sẽ thay các giá trị đã biết vào công thức trên:
A = sin(α+3π/8) . cos(α+π/8) + sin(β-5π/12) . sin(β-π/12) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12)) = (sinα . cos(3π/8) + cosα . sin(3π/8)) . (cosα . cos(π/8) - sinα . sin(π/8)) + (sinβ . cos(5π/12) - cosβ . sin(5π/12)) . (cosβ . cos(π/12) + sinβ . sin(π/12))
Tuy nhiên, để tính giá trị chính xác của A, cần biết thêm giá trị cụ thể của α và β. Trong câu hỏi của bạn, không có thông tin về α và β, do đó không thể tính toán giá trị của A.

Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay vào P ta được

a) Ta có: \(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\cos^2\alpha=1-\dfrac{9}{25}=\dfrac{16}{25}\)
Ta có: \(A=5\cdot\sin^2\alpha+6\cdot\cos^2\alpha\)
\(=5\left(\sin^2\alpha+\cos^2\alpha\right)+\cos^2\alpha\)
\(=5+\dfrac{16}{25}=\dfrac{141}{25}\)
⇔ cosα + sinα = 5(cosα - sinα)
⇔ cosα + sinα = 5cosα - 5sinα
⇔ 6sinα = 4cosα