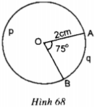
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính diện tích hình quạt tròn OAqB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
17 tháng 8 2018
Đúng(0)
Những câu hỏi liên quan
PT
1
20 tháng 3 2016
* Số đo cung nhỏ AB=góc AOB( góc ở tâm)\(\Rightarrow\) Số đo cung nhỏ AB=60 độ
* Diện ích hình quạt tròn OAB là
\(S=\frac{\pi\times R2\times n}{360}=\frac{\pi\times9\times60}{360}=\frac{3}{2}\pi\approx\frac{3}{2}\times3,14\approx4,71\)cm2
* Số đo cung lớn AB= 360 độ - 60 độ =300 độ
Độ dài cung lớn AB là:
l=3,14*3*300/180=15,7 cm
30 tháng 6 2023
\(S_{quạt\left(OAB\right)}=\dfrac{pi\cdot6^2\cdot120}{360}=12pi\)
CM
4 tháng 6 2019
Thể tích cái phễu là V = 1 3 πr 2 h
Ta có chu vi đáy là 2 πr = Rx
Suy ra
r = R x 2 π h = R 2 - r 2 = R 2 - R 2 x 2 4 π 2 = R 2 π 4 π 2 - x 2
Áp dụng bất đẳng thức AM-GM cho 2 số dương ta có:
V = 3 R 3 48 π 2 x 2 . 2 3 π 4 π 2 - x 2 ≤ 3 R 3 2 . 48 π 2 x 2 4 3 π 2 + 4 π 2 - x 2 = 3 R 3 2 . 48 π 2 x 2 16 3 π 2 - x 2 ≤ 1 8 3 R 3 48 π 2 . x 2 + 16 3 π 2 - x 2 2 = 1 8 3 R 3 48 π 2 . 16 2 9 π 4 = 2 3 27 πR 3
Dấu bằng có khi và chỉ khi
2 3 π = 4 π 2 - x 2 x 2 = 16 3 π 2 - x 2 ⇔ x = 2 2 3 π
Vậy 2 3 27 πR 3 khi và chỉ khi x = 2 2 3 πR 3
Đáp án A
CM
6 tháng 1 2018
Hình tròn bán kính R (ứng với cung 360o) có diện tích là πR2
Vậy hình quạt tròn bán kính R, cung 1o có diện tích là (πR2)/360
Hình quạt tròn bán kính R, cung no có diện tích S = (πR2n)/360