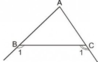
Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài B1 và C1 (h.32) nằm trên tia phân giác của góc A.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2022
-Gọi p/g 2 góc ngoài của góc B và C lần lượt là Bx, Cy và chúng cắt nhau tại D.
-Kẻ DM⊥AB tại M, DN⊥AC tại N, DK⊥BC tại K.
-Theo định lí về t/c của đg p/g của 1 góc \(\Rightarrow DM=DK=DN\)
\(\Rightarrow\)AD là p/g trong góc A (định lí đảo về t/c của đg p/g của 1 góc)
7 tháng 4 2022
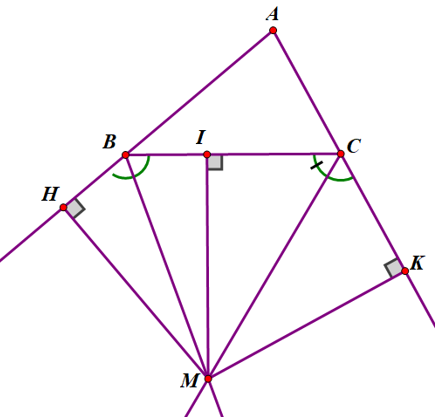
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
=>MH = MK (cùng= MI)
⇒ M thuộc phân giác của góc BAC
DH
13 tháng 4 2016
Hướng dẫn :
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
( H ∈ AB, I ∈ BC, K ∈ AC)
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK
=> M thuộc phân giác của góc
T
18 tháng 4 2019
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).
TT
16 tháng 4 2021
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
Theo định lí thuận về tính chất các điểm thuộc tia phân giác:
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
⇒ M thuộc phân giác của góc BAC (định lí đảo về tính chất các điểm thuộc tia phân giác)
OM
16 tháng 4 2021
Gọi M là giao điểm của 2 tia phân giác 2 góc ngoài B,C
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC ( H ∈ AB, I ∈ BC, K ∈ AC)
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài)
MI = MK (Vì M thuộc phân giác của góc C ngoài)
Suy ra : MH = MK => M thuộc phân giác của góc A
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
Theo định lí thuận về tính chất các điểm thuộc tia phân giác: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí đảo về tính chất các điểm thuộc tia phân giác: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).