Chứng minh định lí "Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn" theo gợi ý sau:
Cho tam giác ABC có góc B > góc C.
a, Có thể xảy ra AC < AB hay không?
b, Có thể xảy ra AC = AB hay không?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 2 2018
Nếu AB > AC thì ∠C > ∠B (góc đối diện với cạnh lớn hơn là góc lớn hơn)
Điều này trái với giả thiết ∠B > ∠C nên không xảy ra.
CM
28 tháng 5 2017
Nếu AB = AC thì ΔABC cân tại A
⇒ ∠B = ∠C(tính chất tam giác cân)
Điều này trái với giả thiết ∠B > ∠C nên không xảy ra.
Vậy nếu ∠B > ∠C thì AC > AB.
15 tháng 8 2017
Khi so sánh AB và AC sẽ có 3 trường hợp xảy ra: AC < AB; AC = AB; AC > AB
+ Nếu AC < AB
Xét tam giác ABC có AC < AB
=> góc B < góc C ( quan hệ giữa cạnh và góc đối diện trong tam giác )
=> Trái với giả thiết góc B > góc C => vô lý
+ Nếu AC = AB
AC = AB => Tam giác ABC cân tại A ( dấu hiệu nhận biết )
=> góc B = góc C ( tính chất )
=> Trái với giả thiết góc B > góc C => vô lý
Vậy nếu tam giác ABC có góc B > góc C thì AC > AB ( đpcm )
17 tháng 9 2023
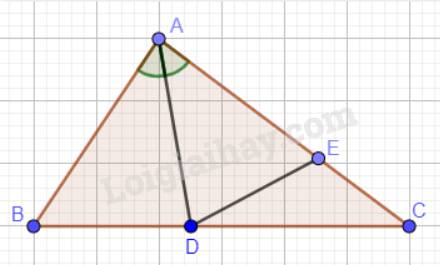
a) Xét hai tam giác ABD và AED: AB = AE, AD chung, \(\widehat {BAD} = \widehat {EAD}\)(AD là phân giác của góc BAC).
Vậy \(\Delta ABD = \Delta AED\) (c.g.c)
b) Ta có: \(\Delta ABD = \Delta AED \Rightarrow \widehat {ABD} = \widehat {AED}\) (2 góc tương ứng)
Ba điểm A, E, C thẳng hàng nên \(\widehat {AED} = 180^\circ \).
Vậy \(\widehat {ABD} = \widehat {AED} = 180^\circ - \widehat {DEC} = \widehat {EDC} + \widehat {ECD}\)(Tổng ba góc trong tam giác EDC bằng 180°).
Do đó, góc B bằng tổng của góc EDC và góc C. Vậy \(\widehat B > \widehat C\).
10 tháng 3 2017
a) TH1 : nếu AC < AB thì góc B < góc C ( trái vs gt )
b) TH2 : Nếu AC = AB thì hai góc B = góc C ( trái vs gt ) *tam giác cân *
Vậy nếu AC> AB thì góc B lớn hơn góc C