Kim tự tháp Louver được xây dựng ngay lối vào của bảo tàng Louvre tại thủ đô Paris nước Pháp. Kim tự tháp có dạng hình chóp đều S.ABCD với chiều cao và chiều dài cạnh bên của kim tự tháp lần lượt là 21m và 34m. Tính thể tích của kim tự tháp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


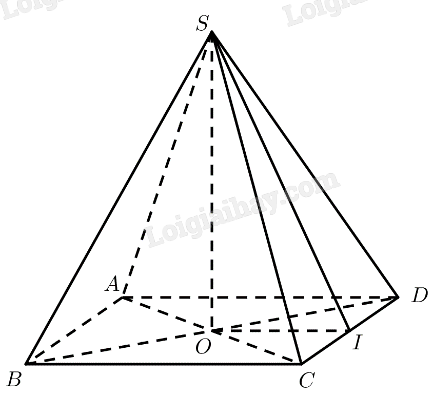
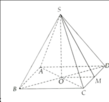
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều \(S.ABC{\rm{D}}\) có \(O\) là tâm của đáy. Kẻ \(SI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right)\).
Ta có: \(SO = 21,6;C{\rm{D}} = 34\)
\(AC = \sqrt {A{B^2} + B{C^2}} = 34\sqrt 2 \Rightarrow OC = \frac{1}{2}AC = 17\sqrt 2 \)
\(\Delta SOC\) vuông tại \(O\)\( \Rightarrow SC = \sqrt {S{O^2} + O{C^2}} \approx 32,3\)
Vậy độ dài cạnh bên bằng \(32,3\left( m \right)\)
Tam giác \(SCD\) cân tại \(S\)
\( \Rightarrow SI\) vừa là trung tuyến, vừa là đường cao của tam giác
\( \Rightarrow I\) là trung điểm của \(CD\).
Mà \(O\) là trung điểm của \(AD\)
\( \Rightarrow OI\) là đường trung bình của tam giác \(ACD\)
\( \Rightarrow OI = \frac{1}{2}BC = 17\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI\)
\( \Rightarrow \Delta SOI\) vuông tại \(O\)\( \Rightarrow SI = \sqrt {S{O^2} + O{I^2}} \approx 27,5\)
\({S_{SC{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.SI \approx 467,5\)
Diện tích xung quanh của kim tự tháp là: \({S_{xq}} = 4{S_{SC{\rm{D}}}} \approx 1870\left( {{m^2}} \right)\)

Thể tích của kim tự tháp là: \(\frac{1}{3}{.34^2}.21,3 = 8207,6\) (\({m^3}\))

Đáp án A
Thể tích của Kim tự tháp là V = 1 3 S h = 1 3 .147.230 2 = 2592100 m 3

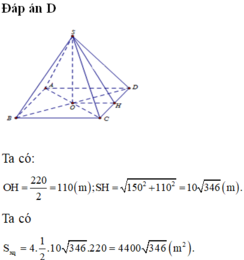
Đáp án D
Ta có: O H = 220 2 = 110 m ; S H = 150 2 + 110 2 = 10 346 m .
Ta có S x q = 4. 1 2 .10 346 .220 = 4400 346 m 2 .



Tương tự 3A
Độ dài cạnh đáy của kim tự tháp là:
Thể tích của kim tự tháp là: 10010 (m3)