Một quả cầu mặt ngoài hoàn toàn không bị nước làm dính ướt. Biết bán kính của quả cầu là 0,1cm, suất căng bề mặt của nước là 0,073N/m.
A. F m a x = 4 , 6 N
B. F m a x = 4 , 5 . 10 - 2 N
C. F m a x = 4 , 5 . 10 - 3 N
D. F m a x = 4 , 6 . 10 - 4 N
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lực căng mặt ngoài tác dụng lên quả cầu: F = σ . l
F cực đại khi l = 2 π r (chu vi vòng tròn lớn nhất)
Vậy F max = 2 π r . σ = 6 , 28.0 , 0001.0 , 073 = 0 , 000046 N ⇒ F max = 46.10 − 6 N
Quả cầu không bị chìm khi trọng lực P = mg của nó nhỏ hơn lực căng cực đại nếu bỏ qua sức đẩy Ac-si-met.
⇒ m g ≤ F max ⇒ m ≤ F max g = 46.10 − 6 9 , 8 = 4 , 694.10 − 6 ( k g ) ⇒ m ≤ 4 , 694.10 − 3 g

a) Lực căng mặt ngoài lớn nhất: F = s.2p.r = 9,2.10-5 N.
b) Quả cầu không bị chìm khi: P £ F = 9,2.10-5 N.

Đáp án: A
Lực căng mặt ngoài lớn nhất tác dụng lên quả cầu:
F = s.2p.r = 9,2.10-5 N.
Quả cầu không bị chìm khi:
![]()

Đáp án A.
Lực căng mặt ngoài lớn nhất tác dụng lên quả cầu: F = σ.2π.r = 9,2. 10 - 5 N.
Quả cầu không bị chìm khi: P ≤ F = 9,2. 10 - 5 N.

![]()
![]()
![]()
![]()
Quả cầu không bị chìm khi trọng lượng P = mg của nó nhỏ hơn lực căng cực đại:
![]()

Ta có: với nước: h 1 = 2 α 1 D 1 g r
với rượu: h 2 = 2 α 2 D 2 g r
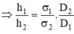
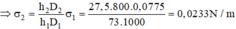

Ta có: h 1 = 2 σ 1 D 1 g r ; h 2 = 2 σ 2 D 2 g r ⇒ h 1 h 2 = σ 1 σ 2 . D 2 D 1 ⇒ σ 2 = h 2 D 2 h 1 D 1 σ 1
Với h 1 = 146 m m , h 2 = 55 m m , D 1 = 10 3 k g / m 3 , D 2 = 800 k g / m 3
σ 1 = 0 , 0775 N / m ⇒ σ 2 = 55.800.0 , 0775 146.1000 = 0 , 0233 N / m

Lực cần thiết để nâng vòng nhôm lên:
F = P + s.2p( r 1 + r 2 ) = hp(r 2 2 - r 1 2 )r + s.2p( r 1 + r 2 ) = 0,0114 N.
Ta có: Lực căng bề mặt tác dụng lên quả cầu : F = σl
F đạt cực đại khi l = 2πr cực đại (chu vi vòng tròn lớn nhất).
→ F m a x = σ 2 π r = 0 , 073 . 2 π . 0 , 1 . 10 - 2 ≈ 4 , 6 . 10 - 4 N
Đáp án: D