Xét sự biến thiên của hàm số y = sinx - cosx. Trong các kết luận sau, kết luận nào đúng?
A. Hàm số đã cho đồng biến trên khoảng ( - π 4 ; 3 π 4 )
B. Hàm số đã cho đồng biến trên khoảng ( 3 π 4 ; 7 π 4 )
C. Hàm số đã cho có tập giá trị là [-1; 1]
D. Hàm số đã cho luôn nghịch biến trên khoảng ( - π 4 ; 7 π 4 )




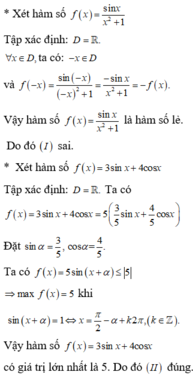

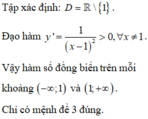

Đáp án A
Ta có y = sin x - cos x = 2 sin x - π 4
Từ đây ta có thể loại đáp án C, do tập giá trị của hàm số là - 2 ; 2
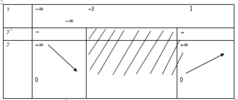
Hàm số đã cho tuần hoàn với chu kỳ 2π do vậy ta xét sự biến thiên của hàm số trên đoạn (-π/4; 7π/4)
Ta có:
* Hàm số đồng biến trên khoảng (-π/4; 3π/4)
* Hàm số nghịch biến trên khoảng (3π/4; 7π/4)