Cho tứ diện S.ABCD. Gọi I và J lần lượt là trung điểm của AC và BC. Trên cạnh BD lấy điểm K sao cho BK= 2 KD.Gọi E là giao điểm của CD với mp (IJK). Tìm mệnh đề đúng.
A. DE= 2 DC
B. DE= DC
C. DC= 2 DE
D. DC= 3 DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 6 2019
Đúng(0)
Những câu hỏi liên quan
KT
18 tháng 12 2016
a) Xét (IJK) và (ACD)
có I thuộc (IJK) giao (ACD)
Trong (BCD) vẽ JK cắt CD tại E
=> E thuộc (IJK) giao (ACD) (đoạn này m ghi tắt :D)
Vậy IE là giao tuyến của (IJK) và (ACD)
Ta có E thuộc IE, IE là con của (IJK)
E thuộc CD
=> E là giao điểm của CD với (IJK)
b) Xét (ABD) và (IJK)
K thuộc (ABD) giao (IJK)
=> Kx là giao tuyến của (ABD) và (IJK)
mà AB // IJ
=> Kx // AB
Trong (ABD) vẽ Kx cắt AD tại F
=> F là giao điểm của AD và (IJK)
Ta có Kx // AB và Kx // IJ (cmt)
mà F thuộc Kx
=> KF // IJ
CM
18 tháng 10 2017
Chọn B.
Phương pháp:
+) Với (P), (Q), (R) là 3 mặt phẳng phân biệt, có
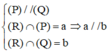
+) Chứng minh hai mặt phẳng song song:
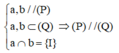
Cách giải:
7 tháng 1
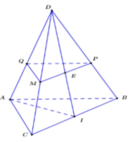
Trong mp(BCD), gọi E là giao điểm của JK và CD
Ta có: \(IE\cap AD=\left\{F\right\}\)
\(IE\subset\left(IJK\right)\)
Do đó: \(AD\cap\left(IJK\right)=F\)
Xét ΔACD có I,F,E thẳng hàng
nên \(\dfrac{AI}{IC}\cdot\dfrac{CE}{ED}\cdot\dfrac{DF}{FA}=1\)
=>\(1\cdot2\cdot\dfrac{DF}{FA}=1\)
=>\(\dfrac{FD}{FA}=\dfrac{1}{2}\)
=>\(\dfrac{FA}{FD}=2\)
CM
1 tháng 9 2017
Đáp án B
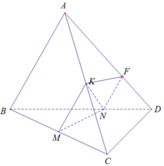
Xét (MNK) và (ABD) có:
N là điểm chung
AB // MK ⇒ A B ⫽ M N K
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua N và song song AB
d cắt AB tại điểm F cần tìm
Vì FN // AB ( cách dựng)
21 tháng 11 2023
Trong mp(BCD), gọi M là giao điểm của KJ với DC
\(M\in KJ\subset\left(IJK\right)\)
\(M\in CD\subset\left(ACD\right)\)
Do đó: \(M\in\left(IJK\right)\cap\left(ACD\right)\left(1\right)\)
\(I\in AC\subset\left(ACD\right);I\in\left(IJK\right)\)
=>\(I\in\left(ACD\right)\cap\left(IJK\right)\left(2\right)\)
Từ (1) và (2) suy ra \(\left(IJK\right)\cap\left(ACD\right)=MI\)
Xét ΔCAB có
\(\dfrac{CI}{CA}=\dfrac{CJ}{CB}=\dfrac{1}{2}\)
nên IJ//AB
\(K\in BD\subset\left(ABD\right);K\in\left(IJK\right)\)
=>\(K\in\left(ABD\right)\cap\left(IJK\right)\)
Xét (ABD) và (IJK) có
\(K\in\left(ABD\right)\cap\left(IJK\right)\)
IJ//AB
Do đó: (ABD) giao (IJK)=xy, xy đi qua K và xy//IJ//AB