Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
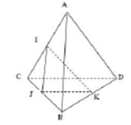
Mặt phẳng (ABD) cắt mặt phẳng (IJK) theo giao tuyến song song với AB do IJ//AB

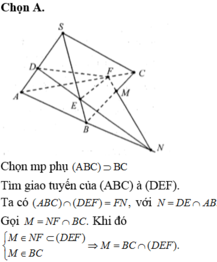
Chọn B.
Phương pháp:
+) Với (P), (Q), (R) là 3 mặt phẳng phân biệt, có
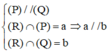
+) Chứng minh hai mặt phẳng song song:
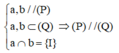
Cách giải:


Đáp án C.


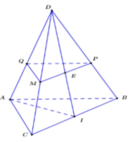
+ (ABD) và (IMK) có điểm chung là k và lần lượt chứa hai đường thẳng AB // MI
=>Giao tuyến của (ABD) và (IMK) là đường thẳng đi qua K và song song với AB và AD tại E =>Thiết diện cần tìm là tứ giác MKEI có M I / / K E M I > K E (1)
+ Δ B M K = Δ A I E ⇒ I E = M K (2)
Từ (1) và (2) =>Tứ giác MKEI là hình thang cân với đáy lớn là MI
+ Có E K = 1 3 ; A B = a 3 ; M I = a 2
Gọi H là hình chiếu vuông góc của E lên MI =>2IH + EK = IM => I H = a 12
I E = A I 2 + A E 2 − 2 A I . A E . c o s 60 ° = a 13 6 ⇒ E H = 13 a 2 36 − a 2 144 = a 51 12
S I M K E = 1 2 E K + I M . E H = 5 a 2 51 144

Đáp án C
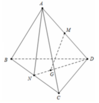
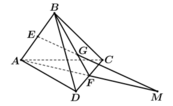
Do 4 điểm A, M, G, N cùng thuộc mặt phẳng (AND) khi đó MG cắt AN suy ra giao điểm của đường thẳng MG và mặt phẳng (ABC) là giao điểm của đường thẳng MG và đường thẳng AN

Bài 2:
a: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó:ABEC là hình bình hành
Suy ra: AC=BE và AC//BE
b: Xét tứ giác AIEK có
AI//KE
AI=KE
Do đó: AIEK là hình bình hành
Suy ra: Hai đường chéo AE và IK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AE
nên M là trung điểm của IK
hay I,M,K thẳng hàng


Đáp án C