Cho tứ diện ABCD có AB=5, các cạnh còn lại bằng 3, khoảng cách giữa hai đường thẳng AB và CD bằng
A. 3 3
B. 2 2
C. 2 3
D. 3 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
3 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
8 tháng 1 2017
Đáp án A
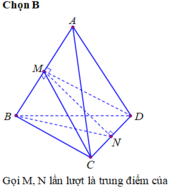
Gọi M, N lần lượt là trung điểm của AB và CD Δ A N B cân tại N nên M N ⊥ A B Δ A D B = Δ A C B c . c . c . Nên M D = M C ⇒ Δ M D C cân tại M ⇒ M N ⊥ C D 2
Từ (1), (2) ta có MN là đoạn vuông góc chung của AB và DC.
Vậy khoảng cách giữa AB và CD bằng MN. M N = A N 2 − A M 2 = 3 3 2 2 − 5 2 2 = 2 2
NM
22 tháng 2 2021
Gọi M, N lần lượt là trung điểm các cạnh AB và CD.
Ta có tam giác ANB cân tại N,
-> MN vuông góc AB.
Tam giác ADB = Tam giác ACB, ta có:
MD=MC -> Tam giác MDC cân tại M.
-> MN vuông góc CD
Do đó ta suy ra MN là đoạn vuông góc chung của cạnh AB và CD.
Ta có khoảng cách từ cạnh AB đến CD là MN:
MN= căn bậc a (AN^2-AM^2)= √2/2
Đáp số: khoảng cách giữa cạnh AB và CD là √2/2
22 tháng 2 2021
Gọi M và N lần lượt là trung điểm của AB và CD. Khi đó:
\(\Delta ACD\)và \(\Delta BCD\)là 2 tam giác đều cạnh 3 nên AN=BN=\(\frac{3\sqrt{3}}{2}\)
Đồng thời \(\Delta ABC=\Delta ABD\)nên CM=DM
Do đó MAB và NCD là 2 tam giác cân tại M và N
Vậy MN _|_ BA và MN _|_ CD
Ta có MN=\(\sqrt{NB^2-MB^2}=\sqrt{\frac{27}{4}-\frac{25}{4}}=\frac{\sqrt{2}}{2}\)
CM
14 tháng 3 2018
Phương pháp
+) Dựng E sao cho ABCE là hình bình hành. Chứng minh d(AB;CD) = d(M;(CDE)).
+) Dựng khoảng cách từ M đến (CDE).
+) Áp dụng định lí Pytago trong các tam giác hình vuông tính CD.
Cách giải
Dựng E sao cho ABCE là hình bình hành như hình vẽ.
CM
25 tháng 11 2017
Chọn đáp án A
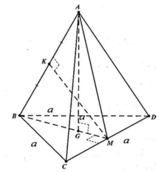
Gọi G là trọng tâm tam giác BCD => AG ⊥ (BCD)
Gọi M là trung điểm CD => BM ⊥ CD
Kẻ MK ⊥ AB (K ∈ AB)
Mặt khác MK ⊥ CD vì CD ⊥ (SBM)
=> MK là đường vuông góc chung.
=> d(AB;CD) = MK
Khi đó M là trung điểm AB
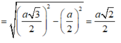
Vậy khoảng cách giữa AB và CD bằng