

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




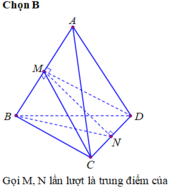
Gọi M, N lần lượt là trung điểm các cạnh AB và CD.
Ta có tam giác ANB cân tại N,
-> MN vuông góc AB.
Tam giác ADB = Tam giác ACB, ta có:
MD=MC -> Tam giác MDC cân tại M.
-> MN vuông góc CD
Do đó ta suy ra MN là đoạn vuông góc chung của cạnh AB và CD.
Ta có khoảng cách từ cạnh AB đến CD là MN:
MN= căn bậc a (AN^2-AM^2)= √2/2
Đáp số: khoảng cách giữa cạnh AB và CD là √2/2

Gọi M và N lần lượt là trung điểm của AB và CD. Khi đó:
\(\Delta ACD\)và \(\Delta BCD\)là 2 tam giác đều cạnh 3 nên AN=BN=\(\frac{3\sqrt{3}}{2}\)
Đồng thời \(\Delta ABC=\Delta ABD\)nên CM=DM
Do đó MAB và NCD là 2 tam giác cân tại M và N
Vậy MN _|_ BA và MN _|_ CD
Ta có MN=\(\sqrt{NB^2-MB^2}=\sqrt{\frac{27}{4}-\frac{25}{4}}=\frac{\sqrt{2}}{2}\)

1:
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt[3]{2-5x}+2}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{10-5x}{\left(x-2\right)\left(\sqrt[3]{2-5x}^2+2\sqrt[3]{2-5x}+4\right)}=\lim\limits_{x\rightarrow2}\dfrac{-5}{\sqrt[3]{2-5x}^2+2\sqrt[3]{2-5x}+4}=-\dfrac{5}{4}\)