Cho x, y > 0 và x + y = 5 4 sao cho biểu thức P = 4 x + 1 4 y đạt giá trị nhỏ nhất. Khi đó
A. x 2 + y 2 = 25 32 .
B. x 2 + y 2 = 17 16 .
C. x 2 + y 2 = 25 16 .
D. x 2 + y 2 = 13 16 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Từ
x + y = 5 4 ⇒ y = 5 4 − x ⇒ P = 4 x + 1 5 − 4 x
Xét
f x = 4 x + 1 5 − 4 x ∀ x ∈ 0 ; 5 4 ⇒ f ' x = − 4 x 2 + 4 5 − 4 x 2
Bảng biến thiên:
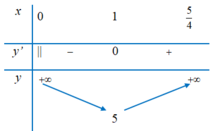
⇒ min f x = 5 khi x = 1 ⇒ y = 1 4 ⇒ x 2 + y 2 = 17 16 .

`A=x^4-6x^3+18x^2-6xy+y^2+2012`
`=x^4-6x^3+9x^2+9x^2-6xy+y^2+2012`
`=(x^2-x)^2+(3x-y)^2+2012>=2012`
Dấu "=" xảy ra khi:
$\begin{cases}x=x^2\\y=3x\end{cases}$
`<=>` $\left[ \begin{array}{l}\begin{cases}x=0\\y=3x=0\\\end{cases}\\\begin{cases}x=1\\y=3x=3\\\end{cases}\end{array} \right.$
Vậy `min_A=2012<=>` $\left[ \begin{array}{l}x=y=0\\\begin{cases}x=1\\y=3\end{cases}\end{array} \right.$

\(Q=\frac{x^3}{4\left(y+2\right)}+\frac{y^3}{4\left(x+2\right)}=\frac{x^3\left(x+2\right)}{4\left(x+2\right)\left(y+2\right)}+\frac{y^3\left(y+2\right)}{4\left(x+2\right)\left(y+2\right)}\)
\(=\frac{x^4+y^4+2x^3+2y^3}{4\left(x+2\right)\left(y+2\right)}=\frac{x^4+y^4+2\left(x+y\right)\left(x^2-xy+y^2\right)}{4\left(xy+2x+2y+4\right)}\)
\(=\frac{x^4+y^4+2\left(x+y\right)\left(x^2-xy+y^2\right)}{4\left(2x+2y+8\right)}=\frac{x^4+y^4+2\left(x+y\right)\left(x^2-xy+y^2\right)}{8\left(x+y+4\right)}\)
Áp dụng bất đẳng thức AM-GM ta có :
\(x^4+y^4\ge2\sqrt{x^4y^4}=2x^2y^2\)
\(x^2+y^2\ge2\sqrt{x^2y^2}=2xy\)
\(Q=\frac{x^4+y^4+2\left(x+y\right)\left(x^2-xy+y^2\right)}{8\left(x+y+4\right)}\ge\frac{2x^2y^2+2xy\left(x+y\right)}{8\left(x+y+4\right)}=\frac{2xy\left(xy+x+y\right)}{8\left(x+y+4\right)}=\frac{8\left(x+y+4\right)}{8\left(x+y+4\right)}=1\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x,y>0\\x=y\\xy=4\end{cases}}\Rightarrow x=y=2\)
Vậy GTNN của Q là 1 <=> x = y = 2
Or
\(Q-1=\frac{\left(x^2-y^2\right)^2+2\left(x+y\right)\left(x^2+y^2-8\right)}{4\left(x+2\right)\left(y+2\right)}\ge0\)*đúng do \(x^2+y^2\ge2xy=8\)*
Do đó \(Q\ge1\)
Đẳng thức xảy ra khi x = y = 2

Áp dụng BĐT Minicopski ta có:
\(T=\sqrt{x^4+\frac{1}{x^4}}+\sqrt{y^2+\frac{1}{y^2}}\ge\sqrt{\left(x^2+y\right)^2+\left(\frac{1}{x^2}+\frac{1}{y}\right)^2}\)
\(\ge\sqrt{1^2+\left(\frac{4}{x^2+y}\right)^2}=\sqrt{1+\left(\frac{4}{1}\right)^2}=\sqrt{17}\)
Nên GTNN của T là \(\sqrt{17}\) khi \(\hept{\begin{cases}x=\sqrt{\frac{1}{2}}\\y=\frac{1}{2}\end{cases}}\)

1/ x = -4
2/ 1007 số hạng
3/ f(2) = 3
4/ 50C = -49
5/ mình ko biết
6/ -1
7/mình cũng đang cần ai giải giúp câu này nếu có người giải thì nhẵn mình với
Bài: Cho x,y >0, x+y>=4. Tìm giá trị nhỏ nhất của biểu thức: A= 3x + 4y +\(\frac{5}{x}+\frac{9}{y}\)

\(A=3x+4y+\frac{5}{x}+\frac{9}{y}=\frac{5}{4}x+\frac{5}{x}+\frac{9}{4}y+\frac{9}{y}+\frac{7}{4}x+\frac{7}{4}y\)
\(\ge2\sqrt{\frac{5}{4}x.\frac{5}{x}}+2\sqrt{\frac{9}{4}y.\frac{9}{y}}+\frac{7}{4}.4\)
\(=5+9+7=21\)
Dấu \(=\)khi \(x=y=2\).