Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
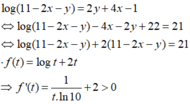
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

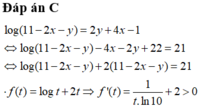
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

Đáp án D
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]

Đáp án D
Cho x,y > 0 thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( 2 + x y ) ⇔ 2 ( x + y ) 2 - ( 2 + x y ) ( x + y ) - 3 x y = 0 (*)
Đặt x + y = u x y = v ta đc PT bậc II: 2 u 2 - ( v + 2 ) u - 3 = 0 gải ra ta được u = v + 2 + v 2 + 28 v + 4 4
Ta có P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 ) = 4 ( x y + y x ) 3 - 9 ( x y + y x ) 2 - 12 ( x y + y x ) + 18 , đặt t = ( x y + y x ) , ( t ≥ 2 ) ⇒ P = 4 t 3 - 9 t 2 - 12 t + 18 ; P ' = 6 ( 2 t 2 - 3 t + 2 ) ≥ 0 với ∀ t ≥ 2 ⇒ M i n P = P ( t 0 ) trong đó t 0 = m i n t = m i n ( x y + y x ) với x,y thỏa mãn điều kiện (*).
Ta có :
t = ( x y + y x ) = ( x + y ) 2 x y - 2 = u 2 v - 2 = ( v + 2 + v 2 + 28 v + 4 ) 2 16 v - 2 = 1 16 ( v + 2 v + v + 4 v + 28 ) 2 - 2 ≥ 1 16 ( 2 2 + 32 ) 2 - 2 = 5 2
Vậy m i n P = P ( 5 2 ) = 4 . ( 5 2 ) 2 - 9 ( 5 2 ) 2 - 12 . 5 2 + 18 = - 23 4

áp án B
Ta có: log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 ⇔ y + 1 log 3 x + 1 y + 1 + x − 1 y + 1 = 9
⇔ y + 1 log 3 c + 1 y + 1 + x + 1 y + 1 − 2 y = 11
⇔ y + 1 log 3 c + 1 y + 1 − 2 = 9 − x + 1 y + 1 *
Nếu x + 1 y + 1 > 9 ⇒ V T * > 0 ; V P * < 0
Ngược lại nếu x + 1 y + 1 < 9 ⇒ V T * < 0 ; V P * > 0
Do đó * ⇔ x + 1 y + 1 = 9 ⇔ x y + x + y = 8
Khi đó P = x + y 3 − 3 x y x + y − 57 x + y = x + y 3 − 3 8 − x − y x + y − 57 x + y
Đặt t = x + y ≥ 2 ⇒ f t = t 3 − 3 8 − t t − 57 t = t 3 + 3 t 2 − 81 t
⇒ f ' t = 3 t 2 + 6 t − 81 = 0 ⇒ t = − 1 + 2 7 ⇒ P min = f − 1 + 2 7 = 83 − 112 7 ⇒ a + b = − 29

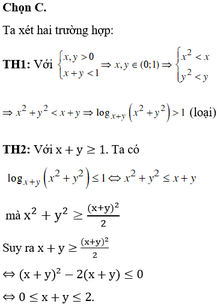
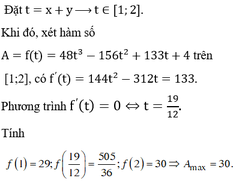

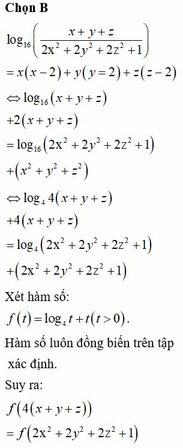


Đáp án B
Từ
x + y = 5 4 ⇒ y = 5 4 − x ⇒ P = 4 x + 1 5 − 4 x
Xét
f x = 4 x + 1 5 − 4 x ∀ x ∈ 0 ; 5 4 ⇒ f ' x = − 4 x 2 + 4 5 − 4 x 2
Bảng biến thiên:
⇒ min f x = 5 khi x = 1 ⇒ y = 1 4 ⇒ x 2 + y 2 = 17 16 .