Tập nghiệm của bất phương trình 1 3 x + 2 > 3 − x
A. 0 ; 2 .
B. 2 ; + ∞ .
C. − 2 ; − 1 .
D. 0 ; + ∞ .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

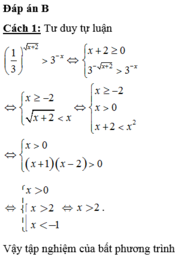



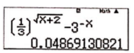

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

1a)
ĐKXĐ :
x\(\ne\)0 ;x+1\(\ne\)0
<=>x\(x\ne0;x\ne-1\)
b)
3/x = 2/x+1
<=>3(x+1) / x(x+1) = 2x / x( x + 1 )
<=>3(x+1)=2x <=> 3x+3=2x
<=>x=-3(thỏa ĐKXĐ)
Vậy S={-3}
2)
\(x+2\ge0\)
<=>\(x\ge-2\)
Vậy S={ \(x\)/\(x\ge-2\)}
0 -2
Vì a>b(1) nên
nhân hai vế bất đẳng thức(1) cho 4 ta được:4a>4b(2)
cộng hai vế bất đẳng thức(2) cho 3 ta được : 4a+3>4b+3

Ta có: \(x-1=0\Rightarrow x=1\),\(x+3=0 \Rightarrow x = - 3\)
BXD:
Vậy \(T=(-\infty;-3]\cup[1;+\infty)\)
- Đặt \(f\left(x\right)=\left(x-1\right)\left(x+3\right)\)
- Cho \(f\left(x\right)=0\Rightarrow\left\{{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
- Lập bảng xét dấu :
x___________-3_________________1______________
x-1____-_____|________-_________0______+___________
x+3___-______0_______+_________|_____+____________
f(x)___+______0_______-__________0_____+____________
- Từ bảng xét dấu :- Để f(x) \(\ge0\)
Vậy phương trình có tập nghiệm \((-\infty;-3]\cup[1;+\infty)\)

Chọn B.
Ta có:
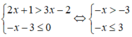
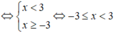
Tập nghiệm của hệ bất phương trình là S = [-3;3).

Ta có: x − 3 x − 2 ≥ 0
Điều kiện: x ≥ 2
Bất phương trình tương đương là x − 3 ≥ 0 x − 2 = 0 ⇔ x ≥ 3 x = 2
Vậy tập nghiệm của bất phương trình là S = { 2 } ∪ [3;+ ∞ )

Ta có: ( x - 3 ) ( x - 2 ) ≥ 0
Điều kiện: x ≥ 2
Bất phương trình tương đương là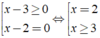
Vậy tập nghiệm của bất phương trình là x = 2 hoặc x ≥ 3