Cho hình lăng trụ đứng có đáy là tam giác đều, có thể tích V. Để diện tích toàn phần của hình lăng trụ nhỏ nhất thì cạnh đáy của lăng trụ bằng
A. 4 V 3
B. V 3
C. 2 V 3
D. 6 V 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 8 2019
Đúng(0)
Những câu hỏi liên quan
CM
18 tháng 7 2019
Đáp án A
Gọi cạnh đáy hình lăng trụ là a, chiều cao là h
⇒ V = S d a y . h = a 2 3 4 . h ⇒ h = 4 V a 2 3
Diện tích toàn phần:
Stoàn phần =S2 đáy +Sxung quanh= a 2 3 2 + 3 a . 4 V a 2 3 = a 2 3 2 + 4 3 V a
Áp dụng bất đẳng thức Cô si:
Stoàn phần = a 2 3 2 + 2 3 V a + 2 3 V a ≥ 3 6 2 . V 2 3
Dấu “=” xảy ra khi a = 4 V 3
CM
16 tháng 2 2019
Đáp án C
Phương pháp:
Thể tích hình lăng trụ V = Sh
Diện tích toàn phần của lăng trụ: Stp = Sxq + 2.Sđáy
Cách giải:
Giả sử hình lăng trụ có đáy là tam giác đều cạnh a, có chiều cao h.
Dấu “=” xảy ra khi và chỉ khi
CM
8 tháng 7 2017
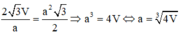
Đáp án D
V A B C D A ' B ' C ' D ' = a 2 b = V ⇒ b = V a 2 ; S t p = 2 a 2 + 4 a b = 2 a 2 + 4 V a = f a
f ' a = 4 a + 4 V a 2 = 0 ⇔ a = V 3 . Lập bảng biến thiên suy ra S t p nhỏ nhất khi V 3
5 tháng 5 2019
a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
5 tháng 5 2019
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
