Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét
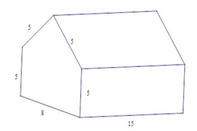
A. 870 m 3
B. 700 m 3
C. 680 m 3
D. 780 m 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 7 2019
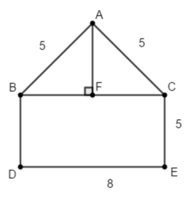
Chia đáy hình ngũ giác ABDEC của lăng trụ đã cho ra thành 2 phần với ABC là tam giác và BDEC là hình chữ nhật như hình vẽ trên.
Nhận thấy tam giác ABC cân tại A, kẻ A F ⊥ B C tại F
Khi đó AF vừa là đường cao vừa là trung tuyến của tam giác ABC
Suy ra BF = CF = 1 2 AC = 1 2 .8 = 4 m
Tam giác AFB vuông tại F, theo định lý Pytago ta có:
A B 2 = A F 2 + F B 2 ⇔ A F 2 = A B 2 − F B 2 = 5 2 − 4 2 = 9
Suy ra AF = 3 m
Do đó diện tích tam giác ABC là: 1 2 B C . A F = 1 2 .8.3 = 12 m 2
Diện tích hình chữ nhật BDEC là: 5.8 = 40 m 2
Diện tích đáy của hình lăng trụ là: 12 + 40 = 52 m 2
Thể tích của nhà kho là:
V = 52.20 = 1040 m 3 .
Đáp án cần chọn là A
CM
22 tháng 1 2018
Thể tích hình lăng trụ đứng (nhà kính) là:
V = S.h = 52.10 = 520 ( m 3 )
CM
5 tháng 6 2018
Theọ hình vẽ, ngôi nhà gồm hai phần,một phần là lăng trụ đứng có đáy là tam giác cân cạnh đáy bằng 6m, chiều cao đáy 1,2m, chiều cao lăng trụ bằng 15m; phần còn lại là hình hộp chữ nhật có kích thước đáy là 6m và 15m, chiều cao 3,5m.
Thể tích hình lăng trụ: V = 1/2 .6.1,2.15 = 54 ( m 3 )
Thể tích hình hộp chữ nhật: V = 6.15.3,5 = 315 ( m 3 )
Vậy thể tích cả ngôi nhà là 54 + 315=369 ( m 3 )
CM
27 tháng 12 2019
Chia hình ABCDE thành hai hình thang vuông có cạnh đáy nhỏ là 5m đáy lớn 8m, chiều cao là 4m.
Ta có: S A B C D E = 2.(5+8)/2 .4 = 52( m 2 )
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}BB' \bot \left( {A'B'C'} \right) \Rightarrow BB' \bot A'B'\\A'B' \bot B'C'\end{array} \right\} \Rightarrow A'B' \bot \left( {CC'B'B} \right)\\ \Rightarrow \left( {CA',\left( {CC'B'B} \right)} \right) = \left( {CA',CB'} \right) = \widehat {A'CB'}\\B'C = \sqrt {BB{'^2} + B{C^2}} = 2\sqrt {61} ,A'B' = AB = 4\\\tan \widehat {A'CB'} = \frac{{A'B'}}{{B'C}} = \frac{2}{{\sqrt {61} }} \Rightarrow \widehat {A'CB'} \approx 14,{4^ \circ }\end{array}\)
Vậy \(\left( {CA',\left( {CC'B'B} \right)} \right) \approx 14,{4^ \circ }\)
b) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot AC,CC' \bot BC\)
Vậy \(\widehat {ACB}\) là góc nhị diện cạnh \(CC'\).
\(\tan \widehat {ACB} = \frac{{AB}}{{AC}} = \frac{1}{3} \Rightarrow \widehat {ACB} \approx 18,{4^ \circ }\)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Diện tích đáy của hình lăng trụ đứng là :
\(\dfrac{1}{2}.\left( {3 + 1,5} \right).1,5 = 3,375\left( {{m^2}} \right)\)
Thể tích (dung tích) của hình lăng trụ đứng là :
\(3,375.2 = 6,75\left( {{m^3}} \right)\)
Chia đáy hình ngũ giác ABDEC của lăng trụ đã cho ra thành 2 phần với ABC là tam giác và BDEC là hình chữ nhật như hình vẽ trên.
Nhận thấy tam giác ABC cân tại A, kẻ A F ⊥ B C tại F
Khi đó AF vừa là đường cao vừa là trung tuyến của tam giác ABC
Suy ra BF = CF = 1 2 AC = 1 2 .8 = 4 m
Tam giác AFB vuông tại F, theo định lý Pytago ta có:
A B 2 = A F 2 + F B 2 ⇔ A F 2 = A B 2 − F B 2 = 5 2 − 4 2 = 9
Suy ra AF = 3 m
Do đó diện tích tam giác ABC là: 1 2 B C . A F = 1 2 .8.3 = 12 m 2
Diện tích hình chữ nhật BDEC là: 5.8 = 40 m 2
Diện tích đáy của hình lăng trụ là: 12 + 40 = 52 m 2
Thể tích của nhà kho là:
V = 52.15 = 780 m 3 .
Đáp án cần chọn là D