Căn bậc hai số học của 25 là:
A. 5
B. – 5
C. ±5
D. 225
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = căn bậc hai của 225 - 1/căn bậc hai của 5 - 1
Tức là :
\(\sqrt{244}\)và \(\sqrt{4}\)
tất nhiên ........
B = căn bậc hai của 196 - 1/căn bậc hai của 6
Tất nhiên ......
2) Tìm GTNN của A = 2 + căn bậc hai của x
\(A=2+\sqrt{x}\)
= \(\sqrt{x+2}\)
3) Tìm GTNN của B = 5 - 2 . căn bậc hai của x - 1
\(B=5-2.\sqrt{x-1}\)
= \(4-2\sqrt{x}\)

a= 2 là căn bậc hai của 4
b = -5 là căn bậc hai của 25;
c = 1 là căn bậc hai của 1
d = 25 là căn bậc hai của 625
e = 0 là căn bậc hai của 0;
g = √7 là căn bậc hai của 7;
h = 3/4 là căn bậc hai của 9/16
i= √4 -3 = 2-3 =-1 là căn bậc hai của 1
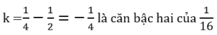


Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
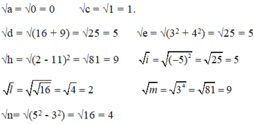

k) Sai
Căn bậc hai của 400 là 20 và -20
l) Đúng
n) Sai
Không có căn bậc hai số học của -16

Sqrt(121)=11
Sqrt(144)=12
Sqrt(169)=13
Sqrt(225)=15
Sqrt(256)=16
Sqrt(324)=18
Sqrt(361)=19
Sqrt(400)=20
Lời giải:
CBHSH:
$\sqrt{121}=11; \sqrt{144}=12; \sqrt{169}=13; \sqrt{225}=15; \sqrt{256}=16; \sqrt{324}=18; \sqrt{361}=19; \sqrt{400}=20$
CBH:
Của $121: \pm 11$
Của $144: \pm 12$
Của $169: \pm 13$
Của $225: \pm 15$
Của $256: \pm 16$
Của $324: \pm 18$
Của $361: \pm 19$
Của $400: \pm 20$
Đáp án là A